Question

15．等腰Rt△ABC中，∠ABC=90°，AB=BC，F为AB上一点，连接CF，过点B作BH⊥CF交CF于G，交AC于H．

（1）如图（1），延长BH到点E，连接AE，当∠EAB=90°，AE=1，F为AB的三等分点，且BF＜AF时，求BE的长；
（2）如图（2），若F为AB中点，连接FH，求证：BH+FH=CF；
（3）如图（3），在AB上取点K，使AK=BF，连接HK并延长与CF的延长线交于点P，若G为CP的中点，请直接写出AH、BH、PG所满足的数量关系．

Answer 1

分析 （1）证明△EAB≌△FBC，得BF=AE=1，由勾股定理求出BE的长；
（2）证明：过点A作AD⊥AB交BH的延长线于点D．推出Rt△BAD≌Rt△CBF，根据全等三角形的性质得到AD=BF，BD=CF．由F为AB的中点，得到AF=BF，等量代换得到AD=AF，证得△AHD≌△AHF，得到DH=FH．根据线段的和差即可得到结论；
（3）作辅助线构建全等三角形和等边三角形，先证明△MAB≌△FBC和△MAH≌△KAH，根据全等三角形性质和三角形内角和定理列等式，求出∠P=30°，由等边△RHB得∠ABH=∠RBC，则△ABH≌△CBR，所以RC=AH，在直角△GHC中利用30°角的余弦列式得出CH=$\frac{CG}{cos30°}$=$\frac{2\sqrt{3}}{3}$CG，即RH+RC=$\frac{2\sqrt{3}}{3}$CG，从而得出结论．

解答 解：（1）∵BH⊥CF，∠ABC=90°，
∴∠ABE+∠CFB=∠CFB+∠BCF=90°，
∴∠ABE=∠BCF，
在△ABE与△BCF中，$\left\{\begin{array}{l}{∠EAB=∠FBC=90°}\\{AB=BC}\\{∠ABE=∠BCF}\end{array}\right.$，
∴△ABE≌△BCF，
∴BF=AE=1，
∵F为AB的三等分点，且BF＜AF，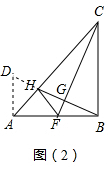
∴AB=3BF=3，
∴BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{10}$；

（2）证明：过点A作AD⊥AB交BH的延长线于点D．
∴∠BAD=∠CBF=90°，
∴∠D+∠ABD=∠CFB+∠ABD=90°，
∴∠ABD=∠BCF，
在△ABD与△BCF中，$\left\{\begin{array}{l}{∠D=∠CFB}\\{∠DAB=∠FBC}\\{AB=BC}\end{array}\right.$，
∴Rt△BAD≌Rt△CBF，
∴AD=BF，BD=CF．
∵F为AB的中点，
∴AF=BF，
∴AD=AF，
在△ADH与△AFH中，$\left\{\begin{array}{l}{AD=AF}\\{∠DAH=∠HAF=45°}\\{AH=AH}\end{array}\right.$，
∴△AHD≌△AHF，
∴DH=FH．
∵BD=BH+DH=BH+FH，
∴BH+FH=CF；
（3）如图4，AH+BH=$\frac{\sqrt{3}}{6}$PG，理由是：
过A作AM⊥AB，交BH延长线于M，
由（2）证得△MAB≌△FBC，
∴AM=BF=AK，∠AMB=∠CFB，
∵△ABC是等腰直角三角形，
∴∠CAB=45°，
∵∠MAB=90°，
∴∠MAH=45°，
∴∠MAH=∠CAB，
在△MAH与△KAH中，$\left\{\begin{array}{l}{AM=AK}\\{∠MAH=∠KAH}\\{AH=AH}\end{array}\right.$，
∴△MAH≌△KAH，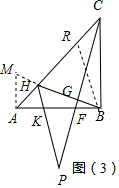
∴∠AMB=∠AKH，
∴∠AKH=∠CFB，
∵∠AKH=∠PKF，∠CFB=∠PFK，
∴∠PKF=∠PFK，
∵FC⊥BH，G是PC中点，
∴CH=PH，
∴∠AHK=2∠P，
在△PFK中，∠PKF=$\frac{180°-∠P}{2}$=90°-$\frac{1}{2}$∠P，
则90°-$\frac{1}{2}$∠P+45°+2∠P=180°，
解得∠P=30°，
在CH上取一点R，使RH=BH，连接BR，
∴∠RHB=$\frac{180°-∠AHK}{2}$=60°，
∴△RHB是等边三角形，
∴BH=BR=RH，
∵∠CAB=∠ACB=45°，∠AHB=180°-60°=120°，∠BRC=180°-60°=120°，
∴∠ABH=∠RBC，
在△ABH与△CBR中，$\left\{\begin{array}{l}{∠ABH=∠CBR}\\{AB=BC}\\{∠BAH=∠BCR}\end{array}\right.$，
∴△ABH≌△CBR，
∴AH=CR，
∵cos30°=$\frac{CG}{CH}$，
∴CH=$\frac{CG}{cos30°}$=$\frac{2\sqrt{3}}{3}$CG，
∴RH+RC=BH+AH=$\frac{2\sqrt{3}}{3}$CG，
∵PG=CG，
∴BH+AH=$\frac{2\sqrt{3}}{3}$CG．

点评 本题是三角形的综合题，考查了等腰直角三角形、全等三角形、等腰三角形等图形的性质和判定，综合性较强；在第一问中，F为AB的三等分点时，要分两种情况进行讨论，根据勾股定理和平行线分线段成比例定理得出结论；在证明两条线段相等时，如果不能直接得出，可以考虑利用第三线段得出，也可以利用等式的性质和线段的和差关系得出，本题的后两问就是利用了这个方法．