
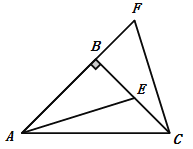
【题目】如图,在△ABC中,AB=BC, ∠ABC=90°,F为AB 延长线上的一点,点E在BC上,且AE=CF.
(1)求证: △ABE≌△CBF.
(2)若∠CAE=15°,求∠ACF的度数.
【答案】(1)证明见解析;(2)75°
【解析】试题分析:(1)根据“HL”即可判定:△ABE≌△CBF;
(2)由等腰直角三角形的性质得到∠BCA=45°,再由∠CAE=15°,得到∠BAE=30°,由全等三角形的性质得到∠BCF的度数,即可得到结论.
试题解析:(1)证明:∵∠ABC=90°,∴△ABE与△CBF为直角三角形.
在Rt△ABE与Rt△ BCF中,∵AB=BC,AE=CF,∴Rt△ABE≌Rt△ BCF;
(2) ∵ AB=BC, ∠ABC=90°,∴∠BCA=∠BAC=45°.
∵∠CAE=15°,∴∠BAE=30°.
∵△ABE≌△CBF,∴∠BCF=∠BAE=30°,∴∠ACF=75°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
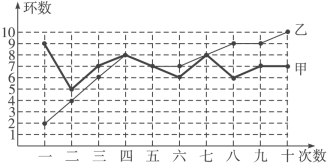
【题目】甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
(1)请填写下表:
平均数 | 方差 | 中位数 | 命中9环及以上的次数 | |
甲 | 7 | 1.2 | 1 | |
乙 | 5.4 |
(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看;
②从平均数和中位数相结合看(分析谁的成绩好些);
③从平均数和命中9环以上的次数相结合看(分析谁的成绩好些);
④从折线图上两人射击命中环数的走势看(分析谁更有潜力).
查看答案和解析>>
科目:初中数学 来源: 题型:
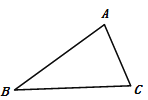
【题目】如图,点A,B,C表示某公司三个车间的位置,现在要建一个仓库,要求它到三个车间的距离相等,则仓库应建在( )
A. △ABC三边的中线的交点上 B. △ABC三内角平分线的交点上
C. △ABC三内高线的交点上 D. △ABC三边垂直平分线的交点上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用简便方法计算,将98×102变形正确的是( )
A. 98×102=1002+22B. 98×102=(100﹣2)2
C. 98×102=1002﹣22D. 98×102=(100+2)2
查看答案和解析>>
科目:初中数学 来源: 题型:
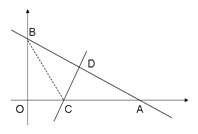
【题目】如图:一次函数y=-![]() x+6的图象与x轴和y轴分别交于点A和B ,再将△ AOB沿直线CD对折,使点A与点B重合。直线CD与x轴交于点C,与AB交于点D.
x+6的图象与x轴和y轴分别交于点A和B ,再将△ AOB沿直线CD对折,使点A与点B重合。直线CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 ,点B的坐标为 。
(2)求OC的长度 ;
(3)在x轴上有一点P,且△PAB是等腰三角形,不需计算过程,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2010年4月14日上午7时49分,我国青海省玉树藏族自治州玉树县发生里氏7.1级的强烈地震,地震造成重大人员伤亡和财产损失.“地震无情,人间有爱”,某慈善机构将募捐得到的两批物资第一时间迅速运往灾区,第一批共480吨,用8节火车皮和20辆汽车正好装完;第二批共524吨,用10节火车皮和6辆汽车正好装完,求每节火车皮和每辆汽车平均各装多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com