
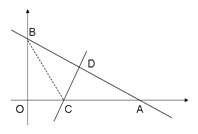
【题目】如图:一次函数y=-![]() x+6的图象与x轴和y轴分别交于点A和B ,再将△ AOB沿直线CD对折,使点A与点B重合。直线CD与x轴交于点C,与AB交于点D.
x+6的图象与x轴和y轴分别交于点A和B ,再将△ AOB沿直线CD对折,使点A与点B重合。直线CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 ,点B的坐标为 。
(2)求OC的长度 ;
(3)在x轴上有一点P,且△PAB是等腰三角形,不需计算过程,直接写出点P的坐标.
【答案】(1)点A的坐标为(4,0),点B的坐标为(0,3)(2)OC=![]() ;(3)p点坐标为(
;(3)p点坐标为(![]() ,0),(-4,0),(-1,0),(9,0)
,0),(-4,0),(-1,0),(9,0)
【解析】试题分析:(1)根据函数图象得出点A和点B的坐标;(2)设OC=x,则AC=CB=4-x,根据Rt△AOB的勾股定理得出x的值,从而得出OC的长度;(3)设点P的坐标为(x,0),然后根据PA=PB,PA=AB,PB=AB三种情况分别求出x的值,从而得到点P的坐标.
试题解析:(1)易知A点坐标y=0,B点坐标x=0,代入y=-![]() x+3可得:A(4,0)B(0,3)
x+3可得:A(4,0)B(0,3)
(2)设OC=x,则AC=CB=4-x
∵∠BOA=900∴OB2+OC2=CB2 ∴32+x2=(4-x)2解得![]() ∴OC=
∴OC=![]()
(3)设P点坐标为(x,0),当PA=PB时,![]() 解得x=
解得x=![]()
当PA=AB时,![]() 解得x=9或x=-1;
解得x=9或x=-1;
当PB=AB时,![]() 解得x=-4.
解得x=-4.
p点坐标为(![]() ,0),(-4,0),(-1,0),(9,0)
,0),(-4,0),(-1,0),(9,0)


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】有理数﹣22 , (﹣2)3 , ﹣|﹣2|, ![]() 按从小到大的顺序排列为( )
按从小到大的顺序排列为( )
A.(﹣2)3<﹣22<﹣|﹣2|< ![]()
B.![]() <﹣|﹣2|<﹣22<(﹣2)3
<﹣|﹣2|<﹣22<(﹣2)3
C.﹣|﹣2|< ![]() <﹣22<(﹣2)3
<﹣22<(﹣2)3
D.﹣22<(﹣2)3< ![]() <﹣|﹣2|
<﹣|﹣2|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程5(2x+5)2+(3x-4)(-3x-4)=11x2+50x+41的解是( )
A. x=2 B. x=-2 C. x=±2 D. 原方程无解
查看答案和解析>>
科目:初中数学 来源: 题型:
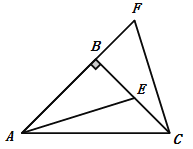
【题目】如图,在△ABC中,AB=BC, ∠ABC=90°,F为AB 延长线上的一点,点E在BC上,且AE=CF.
(1)求证: △ABE≌△CBF.
(2)若∠CAE=15°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线y=3x2先向上平移2个单位,再向右平移3个单位,所得的抛物线是( )
A.y=3(x+3)2﹣2
B.y=3(x+3)2+2
C.y=3(x﹣3)2﹣2
D.y=3(x﹣3)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
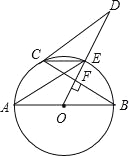
【题目】如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE、AE、CD,若∠AEC=∠ODC.
(1)求证:直线CD为⊙O的切线;
(2)若AB=5,BC=4,求线段CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com