
【题目】用代入消元法解下列方程
(1)![]() (2)
(2) ![]()
(3)![]() (4)
(4)![]()
(5)![]() (6)
(6)![]()
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)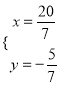 ;(5)
;(5)![]() ;(6)
;(6)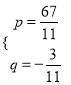 .
.
【解析】试题分析:(1) 把②代入①即可求出y,把y的值代入②即可求出x;
(2)把①代入②即可求出x, 把x的值代入①即可求出y.
(3)把①变形得到y=2x-5,再代入②得到x的值,再把x的值代入y=2x-5求得y的值.
(4)把①变形得到x=5+3y,再代入②得到y的值,再把y的值代入x=5+3y求得x的值.
(5)把①代入②即可求出x, 把x的值代入①即可求出y.
(6)把②变形得到p=5-4q,再代入①得到q的值,再把q的值代入p=5-4q求得p的值.
试题解析:
(1) ![]()
把②代入①得:3y+12y=0,
解得:y=1,
把y=1代入②得:x+2=0,
x=2,
即方程组的解为![]() .
.
(2)![]()
将①代入②,
(x3)2x=5,
x=8,
把x=8代入①,
y=11,
∴方程组的解为![]() .
.
(3)![]()
由①得,y=2x-5 ③
把③代入②得x+2x-5=1
解得x=2
把x=2代入①得2×2-y=5
解得y=-1
∴方程组的解为![]() .
.
(4) ![]()
由①得,x=5+3y,③
把③代入②得2(5+3y)+y=5,
解得y=![]() ,
,
代入①得,x3×(57)=5,
解得x=![]() .
.
故原方程组的解为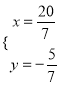 .
.
(5) ![]()
把①代入②得:2x+3(x-3)=6,
解得:x=3,
把x=3代入①得:y=0,
即方程组的解为![]() .
.
(6)![]()
由②得,p=5-4q,③
把③代入①得2(5-4q)-3q=13,
解得![]() ,
,
代入③得,p=5-4×(![]() ),
),
解得![]() .
.
故原方程组的解为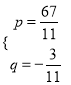 .
.


科目:初中数学 来源: 题型:
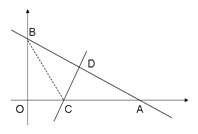
【题目】如图:一次函数y=-![]() x+6的图象与x轴和y轴分别交于点A和B ,再将△ AOB沿直线CD对折,使点A与点B重合。直线CD与x轴交于点C,与AB交于点D.
x+6的图象与x轴和y轴分别交于点A和B ,再将△ AOB沿直线CD对折,使点A与点B重合。直线CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 ,点B的坐标为 。
(2)求OC的长度 ;
(3)在x轴上有一点P,且△PAB是等腰三角形,不需计算过程,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解该校七年级学生的身高情况,抽样调查了部分同学,将所得数据处理后,制成扇形统计图和频数分布直方图(部分)如下(每组只含最低值不含最高值,身高单位:cm,测量时精确到1cm):

(1)请根据所提供的信息计算身高在160~165cm范围内的学生人数,并补全频数分布直方图;
(2)样本的中位数在统计图的哪个范围内?
(3)如果上述样本的平均数为157cm,方差为0.8;该校八年级学生身高的平均数为159cm,方差为0.6,那么 (填“七年级”或“八年级”)学生的身高比较整齐.
查看答案和解析>>
科目:初中数学 来源: 题型:
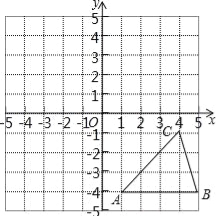
【题目】方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
(1)作出△ABC关于y轴对称的![]() ,并写出
,并写出![]() 的坐标;
的坐标;
(2)作出△ABC绕点O逆时针旋转90°后得到的![]() ,并求出
,并求出![]() 所经过的路径长.
所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(0,8),点B(4,0),连接AB,点M,N分别是OA,AB的中点,在射线MN上有一动点P.若△ABP是直角三角形,则点P的坐标是__.
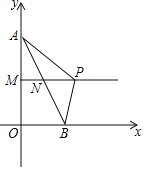
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中, A,B,C 为坐标轴上的三点,且OA=OB=OC=4,过点A 的直线AD 交BC 于点D,交y 轴于点G,△ABD 的面积为8.过点C 作CE⊥AD,交AB 交于F,垂足为E.
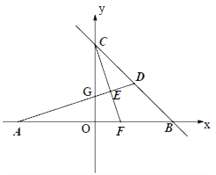
(1)求D 点的坐标;
(2)求证:OF=OG;
(3)在第一象限内是否存在点P,使得△CFP 为等腰直角三角形?若存在,请求出点P 的坐标,若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com