
| A�� | 20���� | B�� | 21���� | C�� | 22���� | D�� | 25���� |
���� �������δ֪����Ȼ����x��ʾ�������������Ĵ��ã�Ȼ����������г�һԪһ�η��̣����x��ֵ���ɣ�
��� �⣺������ס���빫��·��Ϊx���
��������Ϊ10+1.2����x-4����
��������Ϊ8+1.3����x-3����
�������⣬��10+1.2����x-4��+1=8+1.3����x-3����
���x=21��
������ס���빫��·����21���
��ѡB��
���� ������Ҫ������һԪһ�η��̵�Ӧ�ã������Ĺؼ�����δ֪��x��ʾ�����˳˳����շ��ã������ѶȲ���


 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��Rt��ABC�У���ACB=90�㣬��A=35�㣬D��AB��һ�㣬����ABC��CD�۵���ʹB������AC���ϵĴ������ADB1���ڣ�������
��ͼ��Rt��ABC�У���ACB=90�㣬��A=35�㣬D��AB��һ�㣬����ABC��CD�۵���ʹB������AC���ϵĴ������ADB1���ڣ�������| A�� | 10�� | B�� | 15�� | C�� | 20�� | D�� | 30�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
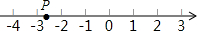 ��ͼ�������ϵ�P��ʾ���������ǣ�������
��ͼ�������ϵ�P��ʾ���������ǣ�������| A�� | $-\sqrt{10}$ | B�� | -3.2 | C�� | $\sqrt{7}$ | D�� | $-\sqrt{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com