解:(1)设抛物线的解析式为y=ax
2+bx+c,
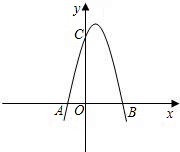
∵抛物线与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C(0,3),
∴

,
解得

,
故抛物线的解析式为y=-

x
2+

x+3;
(2)存在一点P,使△PAB的面积等于△ABC的面积.
∵△ABC的底边AB上的高为3,
∴设△PAB的高为h,则|h|=3,
∵点P在x轴下方,
∴点P的纵坐标为-3,
∴-

x
2+

x+3=-3,
整理得,x
2-3x-8=0,
解得x
1=
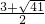
,x
2=
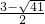
,
∴点P的坐标为(
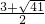
,-3),(
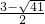
,-3);
(3)∵点B(4,0),点C(0,3),
∴OB=4,OC=3,
根据勾股定理,BC=

=

=5,
①Q
1O=Q
1B时,过Q
1作Q
1D
1⊥x轴于D
1,则点D
1是OB的中点,
∴点Q
1是BC的中点,
∴Q
1(2,

);
②点Q在x轴上方,Q
2B=OB时,过Q
2作Q
2D
2⊥x轴于D
2,
则Q
2D
2=BQ
2sin∠OBC=4×

=

,

BD
2=BQ
2cos∠OBC=4×

=

,
所以,OD
2=OB-BD
2=4-

=

,
所以,Q
2(

,

);
③点Q在x轴下方,Q
3B=OB时,过Q
3作Q
3D
3⊥x轴于D
3,
则Q
3D
3=BQ
3sin∠OBC=4×

=

,
BD
3=BQ
3cos∠OBC=4×

=

,
所以OD
3=OB+BD
3=4+

=

,
所以点Q
3(

,-

);
④Q
4O=OB时,根据等腰三角形三线合一的性质,BQ
4=2•OBcos∠OBC=2×4×

=

,
过Q
4作Q
4D
4⊥x轴于D
4,
则Q
4D
4=BQ
4sin∠OBC=

×

=

,
BD
4=BQ
4cos∠OBC=

×

=

,
所以,OD
4=OD
4-OB=

-4=
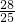
,
所以点Q
4(-
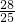
,

);
综上所述,点Q的坐标为Q
1(2,

),Q
2(

,

),Q
3(

,-

),Q
4(-
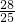
,

).
分析:(1)设抛物线的解析式为y=ax
2+bx+c,把点A、B、C的坐标代入解析式得到关于a、b、c的三元一次方程组,求解即可得到抛物线解析式;
(2)根据等底等高的三角形的面积相等可得点P到AB的距离等于3,再根据点P在x轴下方可知点P的纵坐标为-3,然后代入抛物线解析式求解即可得到点P的横坐标,从而得解;
(3)根据点B、C的坐标求出OB、OC的长度,再根据勾股定理列式求出BC的长度,然后分①Q
1O=Q
1B时,过Q
1作Q
1D
1⊥x轴于D
1,根据等腰三角形三线合一可得点D
1是OB的中点,从而得到点Q
1是BC的中点;②点Q在x轴上方,Q
2B=OB时,过Q
2作Q
2D
2⊥x轴于D
2,利用∠OBC的正弦值求出Q
2D
2的长度,利用余弦值求出BD
2的长度,再求出OD
2,即可得到点Q
2的坐标;③点Q在x轴下方,Q
3B=OB时,过Q
3作Q
3D
3⊥x轴于D
3,根据对顶角相等,利用∠OBC的正弦值求出Q
3D
3的长度,利用余弦值求出BD
3的长度,再求出OD
3,即可得到点Q
3的坐标;④Q
4O=OB时,根据等腰三角形三线合一的性质求出BQ
4的长度,再过Q
4作Q
4D
4⊥x轴于D
4,利用∠OBC的正弦值求出Q
4D
4的长度,利用余弦值求出BD
4的长度,再求出OD
4,即可得到点Q
4的坐标.
点评:本题是二次函数综合题型,主要考查了待定系数法求二次函数解析式,等底等高的三角形的面积相等,等腰三角形的性质以及解直角三角形,(3)要根据等腰三角形的三边中不同的边为腰长进行讨论求解,情况比较复杂,作出图形更形象直观,且不容易漏解.

 如图,已知抛物线与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C(0,3).
如图,已知抛物线与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C(0,3). ,
, ,
, x2+
x2+ x+3;
x+3; x2+
x2+ x+3=-3,
x+3=-3,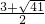 ,x2=
,x2=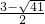 ,
,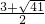 ,-3),(
,-3),(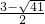 ,-3);
,-3); =
= =5,
=5, );
); =
= ,
,
 =
= ,
, =
= ,
, ,
, );
); =
= ,
, =
= ,
, =
= ,
, ,-
,- );
); =
= ,
, ×
× =
= ,
, ×
× =
= ,
, -4=
-4=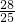 ,
,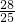 ,
, );
); ),Q2(
),Q2( ,
, ),Q3(
),Q3( ,-
,- ),Q4(-
),Q4(-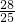 ,
, ).
).

 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).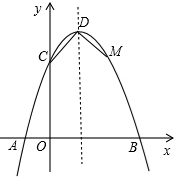 如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1
如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1 函数的最大值是4.
函数的最大值是4.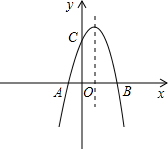 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).