
【题目】如图,在平面直角坐标系中,若每一个方格的边长代表一个单位。
(1)线段CD是线段AB经过怎样的平移得到的?
(2)若C点的坐标是(4,1),A点的坐标是(-1,-2),你能写出B, D三点的坐标吗?
(3)求平行四边形ABCD的面积。
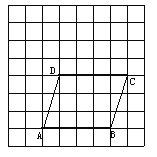
【答案】(1)向上平移3个单位,向右平移1个单位;(2)B(3,-2),D(0,1);(3)12
【解析】
试题分析:(1)根据图形,找到A点与D点,B点与C点的关系,A点如何变化可得D点;将B点相应变化即可;
(2)观察图象,找到D、B与C的位置关系,即可D、B的坐标;
(3)观察图象,可得平行四边形的高与底边长;进而可得平行四边形的面积.
试题解析:(1)向上平移3个单位,向右平移1个单位;
(2)观察图象,找到D、B与C的位置关系,即D点的横坐标是C点的横坐标减4,且其纵坐标相同,即可得D的坐标为(0,1),B点的坐标是C点的横坐标减1,纵坐标减3,故B点坐标为(3,-2);
(3)观察图象,可得平行四边形的高是4;底边长即AB=3;进而可得平行四边形的面积为12.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
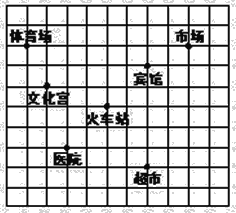
【题目】如图,这是某市部分简图,为了确定各建筑物的位置:
(1)请你以火车站为原点建立平面直角坐标系﹒
(2)写出超市的坐标(小正方形网格的单位长度为1)﹒
(3)请将体育场、宾馆和火车站看作三点,用线段连接起来,得到三角形ABC,然后将此三角形向下平移4个单位,再画出平移后的三角形A′B′C′,并计算三角形A′B′C′的面积﹒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个实数,规定a与b之间的一种运算“⊕”为:a⊕b= ,
,
例如:1⊕(﹣3)=![]() =﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,
=﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,
(x2+1)⊕(x﹣1)=![]() (因为x2+1>0)
(因为x2+1>0)
参照上面材料,解答下列问题:
(1)2⊕4= ,(﹣2)⊕4= ;
(2)若x>![]() ,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE是△ABC的中位线,过点C作CF∥BD交DE的延长线于点F. 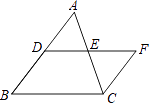
(1)求证:DE=EF.
(2)分别连结DC、AF,若AC=BC,试判断四边形ADCF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com