
 如图,某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上,已知此人的眼睛到地面的距离AB=1.6m,标杆FC=2.2m,且BC=1m,CD=5m,标杆FC、ED垂直于地面.求电视塔的高ED.
如图,某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上,已知此人的眼睛到地面的距离AB=1.6m,标杆FC=2.2m,且BC=1m,CD=5m,标杆FC、ED垂直于地面.求电视塔的高ED. 分析 作AH⊥ED交FC于点G;把实际问题抽象到相似三角形中,利用相似三角形的对应边成比例列出方程,解方程即可.
解答 解:作AH⊥ED交FC于点G;如图所示: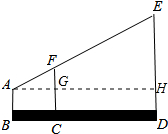
∵FC⊥BD,ED⊥BD,AH⊥ED交FC于点G,
∴FG∥EH,
∵AH⊥ED,BD⊥ED,AB⊥BC,ED⊥BC,
∴AH=BD,AG=BC,
∵AB=1.6,FC=2.2,BC=1,CD=5,
∴FG=2.2-1.6=0.6,BD=6,
∵FG∥EH,
∴$\frac{FG}{EH}=\frac{AG}{AH},\frac{0.6}{EH}=\frac{1}{6}$,
解得:EH=3.6,
∴ED=3.6+1.6=5.2(m)
答:电视塔的高ED是5.2米.
点评 本题考查了相似三角形的应用;通过构造相似三角形.利用相似三角形对应边成比例是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1是边长为20cm的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
如图1是边长为20cm的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).| x(cm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| V(cm3) | 324 | 512 | 588 | 576 | 500 | 384 | 252 | 128 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com