练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．如果规定向北走为正，那么向南走70米可表示为-70米．

    分析 根据题意可以得到向南走70米如何表示．

    解答 解：∵规定向北走为正，
    ∴向南走70米可表示为-70米．
    故答案为：-70米．

    点评 本题考查正数和负数，解题的关键是明确正数和负数在题目中表示的含义．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．如图，某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上，已知此人的眼睛到地面的距离AB=1.6m，标杆FC=2.2m，且BC=1m，CD=5m，标杆FC、ED垂直于地面．求电视塔的高ED．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．拓展探究
    初一年级某班举行乒乓球比赛，需购买5副乒乓球拍，和若干盒乒乓球，现了解情况如下：甲、乙两家商店出售同样品牌的乒乓球拍和乒乓球、乒乓球拍每副定价48元，乒乓球每盒12元，经洽谈后，甲店每买一副乒乓球拍就赠送一盒乒乓球；乙店则全部按定价9折优惠，设该班需购乒乓球x盒（不少于5盒）
    （1）通过计算和化简后，用含x的代数式分别表示甲、乙两店购买所需的费用？
    （2）当需要购40盒乒乓球时，请你去办这件事，你打算去哪家商店购买划算？为什么？
    （3）试探究，当购买乒乓球的盒数x取什么值时去哪家商店购买划算？（直接写出探究的结论）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图所示：残缺的圆形轮片上，弦AB的垂直平分线CD交圆形轮片于点C，垂足为D，解答下列问题：
    （1）用尺规作图找出圆形轮片的圆心O的位置并将圆形轮片所在的圆补全；（要求：保留所有的作图痕迹，不写作法）
    （2）若弦AB=8，CD=3，求圆形轮片所在圆半径R．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．解关于x的方程：b（x-1）=x+1（b≠1），可得x=$\frac{b+1}{b-1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．（1）8+0.25+（-12）-（-$\frac{7}{4}$）
    （2）（1-$\frac{1}{4}$+$\frac{3}{8}$）÷0.125
    （3）-16+（-8）×[$\frac{1}{2}$+（-$\frac{3}{2}$）3]
    （4）（-1$\frac{2}{3}$）÷$\frac{5}{6}$-9×（-$\frac{6}{5}$）-2$\frac{1}{3}$×1.2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

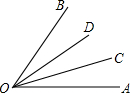    2．如图所示，如果OC，OD是∠AOB的三等分线，那么∠AOC=∠BOD=∠DOC，∠BOD=$\frac{1}{3}$∠AOB，∠AOD=22∠BOD或2∠DOC或2∠COA．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．某商场将进价为20元的某种服装，按60元售出时，每天可以售出20套．据市场调查发现，这种服装每降低1元售价，销量就增加2套，要求售价不得低于成本．
    （1）求每天销售利润y（元）与售价x（元/件）之间的函数表达式．
    （2）当售价为多少时，才能使每天的销售利润最大？最大利润为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知关于x的一元二次方程（m-1）x2+（2m-1）x2+m-$\frac{3}{4}$=0
    （1）若方程有两个相等的实数根时，求m的值．
    （2）当方程有两个实数根时，求出m的最小正整数的值．

    查看答案和解析>>

    同步练习册答案