
����Ŀ����֪������y��ax2+2x��![]() ��a��0����y�ύ�ڵ�A����x���һ������ΪB��
��a��0����y�ύ�ڵ�A����x���һ������ΪB��
��1������ֱ��д����A�������� ����
���������ߵĶԳ���Ϊֱ��x����4ʱ����ֱ��д��a���� ����
��2������BΪ��3��0������m2+2m+3��x��m2+2m+5����am��0ʱ����������͵��������Ϊ��![]() ����m��ֵ��
����m��ֵ��
��3����֪��C����5����3���͵�D��5��1���������������߶�CD��������ͬ�Ľ��㣬��a��ȡֵ��Χ��
���𰸡���1����![]() ����
����![]() ����2��
����2��![]() ����3��a��
����3��a��![]() ��a����3��
��a����3��
��������
��1������x��0���������ߵĽ���ʽ���y��ֵ����ɵ�A�����ꣻ
�����������ߵĶԳ��ṫʽ�г�a�ķ��̣�������a��ֵ��
��2����B��������������ߵĽ���ʽ��������a��ֵ���ٽ����֪����am��0����m��ȡֵ��Χ���ٸ��ݶ��κ��������ʽ��������m2+2m+3��x��m2+2m+5ʱ����������͵��������Ϊ![]() ,�г�m�ķ��̣����m��ֵ�������ó�m��ȷֵ��
,�г�m�ķ��̣����m��ֵ�������ó�m��ȷֵ��
��3���ô���ϵ�������CD�Ľ���ʽ������������ߵĶԳ���![]() �������������������a��0ʱ�������ߵĶ�����y����ߣ�Ҫʹ���������߶�CD��������ͬ�Ľ��㣬��C��D���������������Ϸ���������CD�·���������һ�����г�a����ʽ�飬���н�𣻵�a��0ʱ�������ߵĶ�����y����ұߣ�Ҫʹ���������߶�CD��������ͬ�Ľ��㣬��C��D���������������·��������ߵĶ��������CD�Ϸ����ݴ��г�a�IJ���ʽ����н��
�������������������a��0ʱ�������ߵĶ�����y����ߣ�Ҫʹ���������߶�CD��������ͬ�Ľ��㣬��C��D���������������Ϸ���������CD�·���������һ�����г�a����ʽ�飬���н�𣻵�a��0ʱ�������ߵĶ�����y����ұߣ�Ҫʹ���������߶�CD��������ͬ�Ľ��㣬��C��D���������������·��������ߵĶ��������CD�Ϸ����ݴ��г�a�IJ���ʽ����н��
��1������x��0����![]() ��
��
��![]() ,
,
�ʴ�Ϊ��![]() ��
��
���������ߵĶԳ���Ϊֱ��x����4��
�� ![]() ��
��
��a��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2���ߵ�BΪ��3��0����
��9a+6��![]() ��0��
��0��
��a����![]() ��
��
�������ߵĽ���ʽΪ��![]() ��
��
��Գ���Ϊx����2��
��am��0��
��m��0��
��m2+2m+3��3����2��
�ߵ�m2+2m+3��x��m2+2m+5ʱ��y��x���������С��
�ߵ�m2+2m+3��x��m2+2m+5����am��0ʱ����������͵��������Ϊ��![]() ��
��
�� ![]() ��
��
�����ã�m2+2m+5��2��4��m2+2m+5����12��0��
��ã�m2+2m+5��6����m2+2m+5����2������0���⣩��
��![]() ��
��
��m��0��
��![]() ��
��
��3����ֱ��CD�Ľ���ʽΪy��kx+b��k��0����
�ߵ�C����5����3���͵�D��5��1����
�� ![]() ��
��
��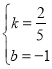 ��
��
��CD�Ľ���ʽΪ![]() ��
��
��y��ax2+2x��![]() ��a��0��
��a��0��
��Գ���Ϊ![]() ��
��
����a��0ʱ��![]() ���������ߵĶ�����y����࣬
���������ߵĶ�����y����࣬
�����������߶�CD��������ͬ�Ľ��㣬
��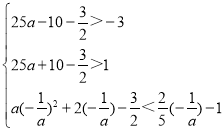 ��
��
��![]() ��
��
����a��0ʱ��![]() ���������ߵĶ�����y����࣬
���������ߵĶ�����y����࣬
�����������߶�CD��������ͬ�Ľ��㣬
��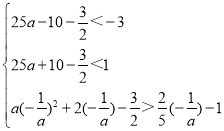 ��
��
��a����3��
���ϣ�![]() ��a����3��
��a����3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ֱ��A��B����ͬʱ��������ͬһ����·�ϣ�������ʻ��������У�����������ʱֹͣ.�׳���ʻһ��ʱ������ͣ��0.5Сʱ�����Ͻ��������ԭ����B����ʻ������֮���·��y��ǧ�ף������������ʱ��x(Сʱ��֮��ĺ�����ϵ��ͼ��ʾ.

��1����ס���������ʻ���ٶ�V����V��.
��2����m��ֵ.
��3�����׳�û�й���ͣ�����������ǰ�ʱ����������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��4��23���ǵڶ�ʮ�ĸ����������������ijУ��֯�������ı��������ѡ��һ���������Ƚ����������������ͼ��ʾ������ͳ��ͼ������ͳ��ͼ�������������������ͼ����Ϣ����������⣺

��1���α�����������������ȫ����ͳ��ͼ��
��2��������ͳ��ͼ�������Ƚ�������Ӧ���ε�Բ�ĽǶ�����
��3��ѧУ�Ӽס��ҡ�������4λһ�Ƚ�������������ȡ2�˲μ��������������������������б�������״ͼ�ķ��������ǡ�ó鵽���ҵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
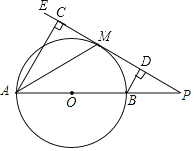
����Ŀ����ͼ��ABΪ��O��ֱ������PΪAB�ӳ����ϵ�һ�㣬����P����O������PE���е�ΪM����A��B����ֱ���PE�Ĵ���AC��BD������ֱ�ΪC��D������AM�������н�����ȷ����___________.(д��������ȷ���۵����)
��AMƽ�֡�CAB��
��AM2��ACAB��
����AB��4����APE��30�㣬��![]() �ij�Ϊ
�ij�Ϊ![]() ��
��
����AC��3��BD��1������CM��DM��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC�Ķ�������ֱ�ΪA����2����4����B��0����4����C��1����2����
��1����ABC����ԭ��O�ԳƵ�ͼ���ǡ�A1B1C1�����û�ͼ����ֱ��д����A1B1C1�Ķ������꣺A1�� ����B1�� ����C1�� ����
��2����ͼ�л�����ABC����ԭ��O��ʱ����ת90����ͼ�Ρ�A2B2C2����ֱ��д����A2B2C2�Ķ������꣺A2�� ����B2�� ����C2�� ����
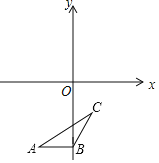
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ڡ�ABC��,AB=AC=10,��D�DZ�BC��һ����(����B,C�غ�),��ADE=��B=��,DE��AC�ڵ�E,��cos��=![]() .���н���:
.�����:
�١�ADE�ס�ACD; �ڵ�BD=6ʱ,��ABD���DCEȫ��;
�ۡ�DCEΪֱ��������ʱ,BDΪ8; ��0<CE��6.4.

������ȷ�Ľ�����____________.(������Ϊ��ȷ���۵���Ŷ�����)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��һö�ʵؾ��ȵ������������ӵ�������ֱ��������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����ͼ2��������
����ͼ2��������![]() �Ķ��㴦����һ��Ȧ����Ȧ��Ϸ�Ĺ���Ϊ����Ϸ��ÿ��һ�����ӣ����ӳ��ϵ������ϵ������Ǽ������������εı߰�˳ʱ�뷽�������������߳����磺����Ȧ
�Ķ��㴦����һ��Ȧ����Ȧ��Ϸ�Ĺ���Ϊ����Ϸ��ÿ��һ�����ӣ����ӳ��ϵ������ϵ������Ǽ������������εı߰�˳ʱ�뷽�������������߳����磺����Ȧ![]() ��������һ������
��������һ������![]() ����˳ʱ��������
����˳ʱ��������![]() ���߳�������Ȧ
���߳�������Ȧ![]() �����ڶ�������
�����ڶ�������![]() ���ʹ�Ȧ
���ʹ�Ȧ![]() ��ʼ˳ʱ��������
��ʼ˳ʱ��������![]() ���߳������Ȧ
���߳������Ȧ![]() ��������Ϸ�ߴ�Ȧ
��������Ϸ�ߴ�Ȧ![]() ����.
����.
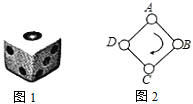
��1��С�������һ�����ӣ�����ص�Ȧ![]() �ĸ���
�ĸ���![]() .
.
��2��С��������������ӣ����б����������ص�Ȧ![]() �ĸ���
�ĸ���![]() ����ָ������С����ص�Ȧ
����ָ������С����ص�Ȧ![]() �Ŀ�����һ����?
�Ŀ�����һ����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������4��23�գ��ǵ�16����������գ�ijУΪ�˽�ѧ��ÿ�ܿ��������Ķ���ʱ�䣬�ڱ�У�����ȡ������ѧ�������ʾ����飬�ֽ����������Ƴ���ͼ��������ͳ��ͼ���������ͼ���е���Ϣ�����������
��� | ѧϰʱ��x��h�� | Ƶ���������� |
A | 0��x��1 | 8 |
B | 1��x��2 | 24 |
C | 2��x��3 | 32 |
D | 3��x��4 | n |
E | 4Сʱ���� | 4 |

��1�����е�n���� ������λ�������� ���飬����ͳ��ͼ��B���Ӧ��Բ�Ľ�Ϊ�� ������
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3����У���ٿ����ÿ���ʱ����������Ķ��Ľ����ᣬ�ƻ���E��ѧ�������ѡ�����˽��о�����ܣ���֪E�������ѧ���У��ߡ����꼶����1�ˣ����꼶��2�ˣ����û���״ͼ�����б������ȡ������ѧ�������Ծ��꼶�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���Ե�OΪԲ�ĵ�����ͬ��Բ�У���Բ����AB��СԲ�ڵ�C��D����ͼ����
��1����֤��AC=BD��
��2������Բ�İ뾶R=10��СԲ�İ뾶r=8����ԲO��ֱ��AB�ľ���Ϊ6����AC�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com