
 红丝带(图1)是对HIV和艾滋病认识的国际符号,1991年在美国纽约第一次出现,它代表了关心,这一标志被越来越多的人佩带,用来表示他们对HIV和艾滋病的关心.现将宽为2cm的长方形纸条折叠成如图2所示的丝带形状,那么折痕PQ的长是$\frac{4\sqrt{3}}{3}$.
红丝带(图1)是对HIV和艾滋病认识的国际符号,1991年在美国纽约第一次出现,它代表了关心,这一标志被越来越多的人佩带,用来表示他们对HIV和艾滋病的关心.现将宽为2cm的长方形纸条折叠成如图2所示的丝带形状,那么折痕PQ的长是$\frac{4\sqrt{3}}{3}$. 分析 由题意可知△EPQ是等边三角形,作QF⊥EP于F,在RT△PQF中利用勾股定理即可求出PQ.
解答 解:由题意可知△EPQ是等边三角形,作QF⊥EP于F,
在RT△PQF中,∵QF=2,∠QPF=60°,∠PFQ=90°,
∴∠PQF=30°,PQ=2PF,设PF=a,则PQ=2a,
∵PQ2=PF2+FQ2,
∴a2+22=(2a)2,
∴a2=$\frac{4}{3}$,
∵a>0,
∴a=$\frac{2\sqrt{3}}{3}$,
∴PQ=$\frac{4\sqrt{3}}{3}$.
故答案为$\frac{4\sqrt{3}}{3}$.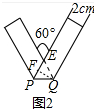
点评 本题考查翻折变换、等边三角形的性质、勾股定理等知识,解题的关键是作等边三角形的高利用勾股定理解决问题,属于中考常考题型.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:填空题
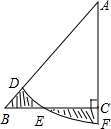 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF2为$\frac{4}{π}$.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF2为$\frac{4}{π}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
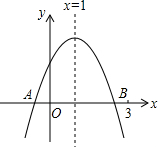 如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,下列结论:
如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,下列结论:| A. | 3个 | B. | 2个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2015}{2016}$ | B. | $\frac{2017}{2016}$ | C. | $\frac{2015}{2017}$ | D. | $\frac{2016}{2017}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,3) | B. | (-1,3) | C. | (3,-1) | D. | (3,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
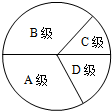 为了解我县1800名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:
为了解我县1800名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:| 等级 | A级(优秀) (≥108分) | B级(良好) (≥84分且<108分) | C级(及格) (≥72分且<84分) | D级(不及格) (<72分) |
| 人数 | 22 | 28 | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com