
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��0��1����D��-2��0������ֱ��AD�����߶�ADΪһ��������������ABCD��
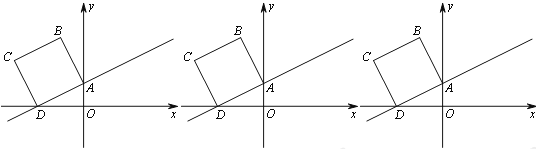
��1����գ���B������Ϊ________����C������Ϊ_________��
��2������������ÿ��![]() ����λ���ȵ��ٶ�������DA����ƽ�ƣ�ֱ�������εĶ���C����y����ʱֹͣ�˶������˶������У�������������y���Ҳಿ�ֵ����ΪS����S����ƽ��ʱ��t�������ĺ�����ϵʽ����д����Ӧ���Ա���t��ȡֵ��Χ��
����λ���ȵ��ٶ�������DA����ƽ�ƣ�ֱ�������εĶ���C����y����ʱֹͣ�˶������˶������У�������������y���Ҳಿ�ֵ����ΪS����S����ƽ��ʱ��t�������ĺ�����ϵʽ����д����Ӧ���Ա���t��ȡֵ��Χ��
���𰸡���1������1��3������2��S= .
.
��������
������������⿼���������ε����ʡ�ȫ�������ε��ж������ʡ�һԪһ�β���ʽ��Ӧ�á������ε������ʽ�Լ�ֱ�����ε������ʽ������Ĺؼ�����1����ȫ�������ε������ҳ���ABB���CC��D���ߵij��ȣ���2����һԪһ�β���ʽ�ҳ���ͬ�����t��ȡֵ��Χ�����������е��⣬��1���ѶȲ�������������⣬���Բ���ȥ֤������ȫ��ʡȥ����ʱ�䣻��2���ѶȲ����ǹ��̷�������������в����õ��˽�һԪһ�β���ʽ��x��ȡֵ��Χ�����õ��������Ρ�ֱ�����ε������ʽ�����ڽ����������Ŀʱ��ϸ�Ĺ۲�ͼ�Σ�ͨ��ͼ�εı仯�����ǹؼ�.
��1������B��BB����y���ڵ�B�䣬����C��CC����x���ڵ�C�䣬��ȫ�������ε����ʿ�֪AB��=CC��=DO��BB��=DC��=AO����ϸ��ߵĹ�ϵ�����ҳ�B��C������ꣻ
��2����ͼ�εı仯�ֳ������֣�����ʱ��t��ʾ��ֱ����������ֱ�DZ߳��ȣ����������������ʽ���ɵó����ۣ�����ʱ��t��ʾ��ֱ�������ϡ��µ���ߵij��ȣ��������ε������ʽ���ɵó����ۣ����������ε������ȥʣ��ֱ�������ε�������ɵó�����.
�����������1������1��3����
��2����0��t��![]() ʱ��S=5t2��
ʱ��S=5t2��
��![]() ��t��1ʱ��S=5t-
��t��1ʱ��S=5t-![]() ��
��
��1��t��![]() ʱ��S=5t2+15t-
ʱ��S=5t2+15t-![]() .
.
���ϣ�S= .
.


 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д� ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһƽ���ڣ�ֱ��a��b�ཻ��P����a��c����b��c��λ�ù�ϵ��________ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P�������ޣ��ҵ�P��x��ľ���Ϊ3����P��y��ľ���Ϊ2�����P������Ϊ�� ��
A.����3����2��
B.��3����2��
C.��2��3��
D.��2����3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ÿ�����ֱ�������ľ���ij��ȣ��������ǰڳ������ε��ǣ�������
A. 3cm��4cm��8cm B. 8cm��7cm��15cm
C. 5cm��5cm��11cm D. 13cm��12cm��20cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��Rt��ABC�У���ABC=90�㣬AB=BC�� BO��AC���ϵ����ߣ���P��D�ֱ���AO��BC�ϣ�PB=PD��DE��AC�ڵ�E��


��1����֤����BPO�ա�PDE��
��2����PBƽ�֡�ABO�������������䣮��֤��AP=CD��
���Ƚ�ͼ�β���������Ȼ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ſ�����ȵľ���ֽƬ������һ��õ���ͼ��ʾ���ı���ABCD.

��1����֤���ı���ABCD�����Σ�
��2��������ž���ֽƬ�ij�����8��������2����ô��DCB������Ƿ�������ֵ����Сֵ��������ڣ������������������ڣ����Ҫ˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A(��1����4)��B(��1��3)����(����)
A. A��B����x��Գ� B. A��B����y��Գ�
C. ֱ��ABƽ����y�� D. ֱ��AB��ֱ��y��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com