
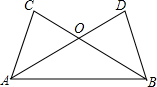
 已知:如图,AD、BC相交于点O,OA=OB,∠C=∠D.
已知:如图,AD、BC相交于点O,OA=OB,∠C=∠D.分析 (1)由对顶角相等可知:∠COA=∠DOB,然后依据AAS证明△AOC≌△BOD即可;
(2)由△AOC≌△BOD可知:CO=DO,由AO=OB,CO=DO可得到AD=BC.
解答 证明:(1)由对顶角相等可知:∠COA=∠DOB,
在△ABC和△BAD中,
$\left\{\begin{array}{l}{∠COA=∠DOB}\\{∠C=∠D}\\{OA=OB}\end{array}\right.$,
∴△ABC≌△BAD.
(2)∵△ABC≌△BAD,
∴OC=OD,
又∵OA=OB,
∴OA+OD=OB+OC,
∴AD=BC.
点评 本题主要考查的是全等三角形的性质和判定,掌握全等三角形的性质和判定定理是解题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
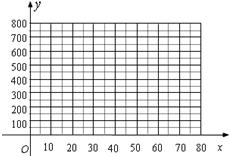 2015年9月19日第九届合肥文博会开幕.开幕前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:
2015年9月19日第九届合肥文博会开幕.开幕前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量(y件) | … | 500 | 400 | 300 | 200 | 100 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
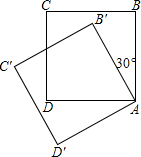 如图,把边长为4的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于$\frac{16\sqrt{3}}{3}$.
如图,把边长为4的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于$\frac{16\sqrt{3}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com