
分析 (1)移项后配方即可解答;
(2)解出不等式,然后即可求出其正整数解.
解答 解:(1)解方程x2-4x+1=0,
移项得,x2-4x=-1,
配方得,x2-4x+4=-1+4,
(x-2)2=3,
开方得,x-2=±$\sqrt{3}$,
解得,x=2±$\sqrt{3}$,
x1=2+$\sqrt{3}$,x2=2-$\sqrt{3}$.
(2)去分母得,3(x-2)≤2(7-x),
去括号得,3x-6≤14-2x,
移项、合并同类项得,5x≤20,
系数化为1得,x≤4,
则其正整数解为1,2,3,4.
点评 (1)本题考查了配方法的一般步骤:
①把常数项移到等号的右边;
②把二次项的系数化为1;
③等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
(2)本题考查了解不等式,熟悉不等式的性质是解题的关键.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:解答题
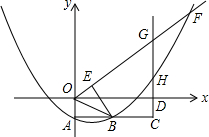 如图,抛物线y=$\frac{1}{2}$x2+mx-n(n>0)与y轴交于点A,过点A作AB∥x轴,交抛物线于点B,延长AB到C,使BC=AB,过点C作CD⊥x轴于点D(4n,0).
如图,抛物线y=$\frac{1}{2}$x2+mx-n(n>0)与y轴交于点A,过点A作AB∥x轴,交抛物线于点B,延长AB到C,使BC=AB,过点C作CD⊥x轴于点D(4n,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是$\frac{3}{10}$ | |
| B. | 随机抛掷一枚均匀的硬币,落地后反面一定朝上 | |
| C. | 某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖 | |
| D. | 在一次课堂进行的抛硬币试验中,同学们估计硬币落地后正面朝上的概率为0.51 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
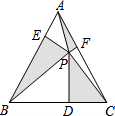 如图,等边△ABC中,P为三角形内一点,过P作PD⊥BC,PE⊥AB,PF⊥AC,连结AP、BP、CP,如果S△APF+S△BPE+S△PCD=$\frac{9\sqrt{3}}{2}$,那么△ABC的内切圆半径为( )
如图,等边△ABC中,P为三角形内一点,过P作PD⊥BC,PE⊥AB,PF⊥AC,连结AP、BP、CP,如果S△APF+S△BPE+S△PCD=$\frac{9\sqrt{3}}{2}$,那么△ABC的内切圆半径为( )| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
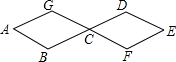 蜜蜂采蜜时,如果蜜源很远它就会跳起“8字舞”,告诉同伴蜜源的方向.如图所示,两个全等菱形的边长为1厘米,一只蜜蜂由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,飞行2015厘米后停下,则这只蜜蜂停在G点.
蜜蜂采蜜时,如果蜜源很远它就会跳起“8字舞”,告诉同伴蜜源的方向.如图所示,两个全等菱形的边长为1厘米,一只蜜蜂由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,飞行2015厘米后停下,则这只蜜蜂停在G点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com