
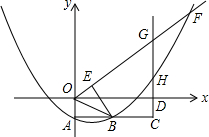
 如图,抛物线y=$\frac{1}{2}$x2+mx-n(n>0)与y轴交于点A,过点A作AB∥x轴,交抛物线于点B,延长AB到C,使BC=AB,过点C作CD⊥x轴于点D(4n,0).
如图,抛物线y=$\frac{1}{2}$x2+mx-n(n>0)与y轴交于点A,过点A作AB∥x轴,交抛物线于点B,延长AB到C,使BC=AB,过点C作CD⊥x轴于点D(4n,0).分析 (1)根据题意求得点B的坐标,把点B的坐标代入函数解析式可以得到m、n之间的数量关系;
(2)①取OG的中点R,连接BR,则易得BR为直角梯形OACG的中位线.欲证明OG为直径的圆必与直线AC相切,只需推知RB是⊙R的半径即可;
②过点E作MN∥x轴,过点B作BN⊥MN.构建相似三角形:△OME∽△ENB,根据该相似三角形的对应边成比例和折叠的性质得到:$\frac{OE}{EB}$=$\frac{OA}{AB}$=$\frac{1}{2}$,则E($\frac{4}{5}$n,$\frac{3}{5}$n);利用待定系数法求得直线OE的表达式根据两直线相交可以求得G(4n,4n2-n).结合图象得到关于n的不等式3n>4n2-n,依此可以得到n的取值范围;
③易求GH=3n-(4n2-n)=-4n2+4n.利用二次函数最值的求法得到n的值,然后再来求二次函数解析式.
解答 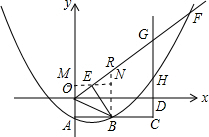 解:(1)∵抛物线y=$\frac{1}{2}$x2+mx-n(n>0)与y轴交于点A,
解:(1)∵抛物线y=$\frac{1}{2}$x2+mx-n(n>0)与y轴交于点A,
∴A(0,-n).
又∵D(4n,0),BC=AB,
∴B(2n,-n).
把点B的坐标代入y=$\frac{1}{2}$x2+mx-n,得
-n=$\frac{1}{2}$×4n2+2mn-n,
整理,得
m+n=0.
故答案是:m+n=0;
(2)①证明:取OG的中点R,连接BR,则易得BR为直角梯形OACG的中位线,
∴RB⊥AC,RB=$\frac{1}{2}$(OA+CG)=$\frac{5}{2}$n.
∵OG=5n,
∴RB是⊙R的半径,即AC为⊙R的切线;
②解:易得A(0,-n),B(2n,-n).
过点E作MN∥x轴,过点B作BN⊥MN.
易证得△OME∽△ENB,
∴$\frac{{y}_{E}}{2n-{x}_{E}}$=$\frac{{x}_{E}}{{y}_{E}+n}$=$\frac{OE}{EB}$.
由折叠可知:$\frac{OE}{EB}$=$\frac{OA}{AB}$=$\frac{1}{2}$,
∴$\left\{\begin{array}{l}{{x}_{E}=\frac{4}{5}n}\\{{y}_{E}=\frac{3}{5}n}\end{array}\right.$,即E($\frac{4}{5}$n,$\frac{3}{5}$n).
∴直线OE的表达式为:y=$\frac{3}{4}$x.
∴直线OE与直线CD交点G的坐标为(4n,8n2+4mn-n),即(4n,4n2-n).
∵直线OE与抛物线的交点F在直线CD的右侧,
∴点G在点H的上方,即3n>4n2-n,
解得:n<1,
∴实数n的取值范围是:0<n<1;
③易得G(4n,3n),则GH=3n-(4n2-n)=-4n2+4n.
当n=$\frac{1}{2}$时,GH取得最大值为1.
∴GH取整数值为1,此时抛物线的表达式为y=$\frac{1}{2}$x2-x-1.
点评 本题考查了二次函数综合题.解题时,利用了待定系数法求函数解析式、函数图象交点的求法、相似三角形的判定与性质以及切线的判定等知识点.主要考查学生数形结合的数学思想方法.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:解答题
 如图,将平面直角坐标系的纵轴绕原点顺时针旋转30°,得到夹角为60°的平面坐标系xOy,称之为平面60°角坐标系.类比平面直角坐标系中确定点的坐标的方法,设平面60°角坐标系中有任意一点P,过点P作PA∥y轴,交x轴于点A,A点的坐标为(x,0),过点P作PB∥x轴,交y轴于点B,B点的坐标为(0,y),则点P坐标为(x,y).
如图,将平面直角坐标系的纵轴绕原点顺时针旋转30°,得到夹角为60°的平面坐标系xOy,称之为平面60°角坐标系.类比平面直角坐标系中确定点的坐标的方法,设平面60°角坐标系中有任意一点P,过点P作PA∥y轴,交x轴于点A,A点的坐标为(x,0),过点P作PB∥x轴,交y轴于点B,B点的坐标为(0,y),则点P坐标为(x,y).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
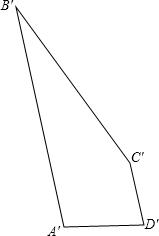 如图所示,四边形A′B′C′D′是将四边形ABCD平移后得到的,已知A′B′=13,B′C′=12,C′D′=3,D′A′=4,求四边形ABCD的周长.
如图所示,四边形A′B′C′D′是将四边形ABCD平移后得到的,已知A′B′=13,B′C′=12,C′D′=3,D′A′=4,求四边形ABCD的周长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
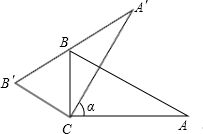 直角三角板ABC中,∠A=30°,BC=2.将其绕直角顶点C逆时针旋转一个角α(0°<α<120°且α≠90°),得到Rt△A′B′C′
直角三角板ABC中,∠A=30°,BC=2.将其绕直角顶点C逆时针旋转一个角α(0°<α<120°且α≠90°),得到Rt△A′B′C′查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 薄板的边长(cm) | 20 | 30 |
| 出厂价(元/张) | 50 | 70 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
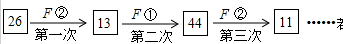
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
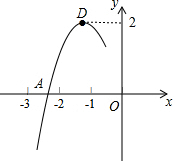 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com