
 ��ͼ����ƽ��ֱ������ϵ��������ԭ��˳ʱ����ת30�㣬�õ��н�Ϊ60���ƽ������ϵxOy����֮Ϊƽ��60�������ϵ�����ƽ��ֱ������ϵ��ȷ���������ķ�������ƽ��60�������ϵ��������һ��P������P��PA��y�ᣬ��x���ڵ�A��A�������Ϊ��x��0��������P��PB��x�ᣬ��y���ڵ�B��B�������Ϊ��0��y�������P����Ϊ��x��y����
��ͼ����ƽ��ֱ������ϵ��������ԭ��˳ʱ����ת30�㣬�õ��н�Ϊ60���ƽ������ϵxOy����֮Ϊƽ��60�������ϵ�����ƽ��ֱ������ϵ��ȷ���������ķ�������ƽ��60�������ϵ��������һ��P������P��PA��y�ᣬ��x���ڵ�A��A�������Ϊ��x��0��������P��PB��x�ᣬ��y���ڵ�B��B�������Ϊ��0��y�������P����Ϊ��x��y�������� ��1������ƽ��60�������ϵ����ȷ��������C�����ꣻ
��2����ͼ1��֤����OAM�ǵȱ������Σ��ı���OAMB�����Σ���ME=MF=$\sqrt{3}$����MOE=60�㣬�õ�OA=OB=2���������M�����ꣻ
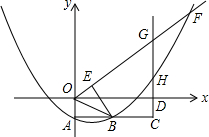
��3����ͼ2�������E��F�����꣬����E��EG��y�ύx���ڵ�G������E��EH��x�ᣬ����ΪH�����EH�����ɼ���ֱ��y=x��ֱ��y=-$\frac{1}{2}$x+$\frac{3}{2}$��x��Χ�ɵ�������Ϊ��OEF�������
��� �⣺��1���߹���A��1��0����B��0��1���ֱ���y�ᡢx���ƽ���ߣ�����ֱ�߽��ڵ�C��
��C��1��1����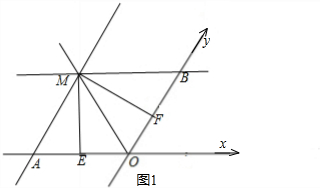
�ʴ�Ϊ��1��1��
��2����ͼ1���ߵ�M�ڵڶ����ޣ���M��x�ᡢy��ľ����Ϊ$\sqrt{3}$��
��OMƽ�ֵڶ����нǣ�
��ME=MF=$\sqrt{3}$����MOE=60�㣬
��OM=2��
�ߡ�AOB=120�㣬�ı���OAMB��ƽ���ı��Σ�
���A=60�㣬
���OAM�ǵȱ������Σ��ı���OAMB�����Σ�
��OA=OB=2��
��M��-2��2����
�ʴ�Ϊ��-2��2�� ��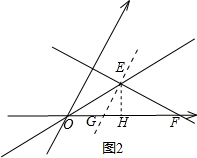
��3����ֱ��y=x��ֱ��y=-$\frac{1}{2}$x+$\frac{3}{2}$���ڵ�E����ͼ2��
�ⷽ����$\left\{\begin{array}{l}{y=x}\\{y=-\frac{1}{2}x+\frac{3}{2}}\end{array}\right.$����$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$��
���E��������1��1����
ֱ�� y=-$\frac{1}{2}$x+$\frac{3}{2}$����y=0����x=3
ֱ��y=-$\frac{1}{2}$x+$\frac{3}{2}$��x��Ľ���ΪF��3��0����
��OF=3��
��ֱ��y=x��ֱ��y=-$\frac{1}{2}$x+$\frac{3}{2}$��x��Χ�ɵ�������Ϊ��OEF��
����E��EG��y�ύx���ڵ�G����OG=1����EGF=60�㣬��EG=1��
����E��EH��x�ᣬ����ΪH����Rt��EGH�У�
EH=EG•sin��EGH=EG•sin60��=$\frac{\sqrt{3}}{2}$��
��S��OEF=$\frac{1}{2}$OF•EH=$\frac{1}{2}$��3��$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{4}$��
���� ������Ҫ�������Ķ��������͵�һ�κ����ۺ��⣬������ĿҪ��ѧ�����н�ǿ���Ķ�����������ģ�������Լ����ν��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABΪֱ���ġ�O����AC���е�D��DE��BC�ڵ�E��
��ͼ����ABΪֱ���ġ�O����AC���е�D��DE��BC�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x+3y=5xy | B�� | x•4x4=4x4 | C�� | x6��x2=x3 | D�� | ��-xy2��3=-x3y6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
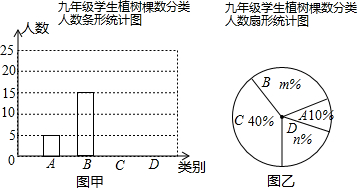
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
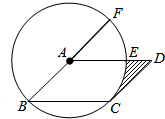 ��ͼ����?ABCD�У��Ե�AΪԲ�ģ�AB�ij�Ϊ�뾶��Բǡ����CD�����ڵ�C����AD�ڵ�E���ӳ�BA���O�ཻ�ڵ�F����$\widehat{EF}$�ij�Ϊ$\frac{��}{2}$����ͼ����Ӱ���ֵ����Ϊ2-$\frac{��}{2}$��
��ͼ����?ABCD�У��Ե�AΪԲ�ģ�AB�ij�Ϊ�뾶��Բǡ����CD�����ڵ�C����AD�ڵ�E���ӳ�BA���O�ཻ�ڵ�F����$\widehat{EF}$�ij�Ϊ$\frac{��}{2}$����ͼ����Ӱ���ֵ����Ϊ2-$\frac{��}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2+x����x+2�� | B�� | ��x+y����y-x�� | C�� | ��-x+y����y-x�� | D�� | ��x2+y����x-y2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2015��-1 | B�� | -��2015��-1 | C�� | ��-1������-2015�� | D�� | ��-2015����2015 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������y=$\frac{1}{2}$x2+mx-n��n��0����y�ύ�ڵ�A������A��AB��x�ᣬ���������ڵ�B���ӳ�AB��C��ʹBC=AB������C��CD��x���ڵ�D��4n��0����
��ͼ��������y=$\frac{1}{2}$x2+mx-n��n��0����y�ύ�ڵ�A������A��AB��x�ᣬ���������ڵ�B���ӳ�AB��C��ʹBC=AB������C��CD��x���ڵ�D��4n��0�����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com