练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．抛物线y=ax2+bx+c经过点A（-5，4），且对称轴是直线x=-2，则a+b+c=4．

    分析 把A点坐标代入抛物线解析式结合对称轴方程可用a分别表示出b和c，则可用a表示出抛物线解析式，再令x=1代入可求得y的值，即a+b+c的值．

    解答 解：∵对称轴方程为x=-2，
    ∴-$\frac{b}{2a}$=-2，整理可得b=4a，
    ∵抛物线y=ax2+bx+c经过点A（-5，4），
    ∴4=25a-5b+c，
    把b=4a代入可得，4=25a-20a+c，解得c=4-5a，
    ∴抛物线解析式为y=ax2+4ax+4-5a，
    当x=1时，则有a+b+c=a+4a+4-5a=4，
    故答案为：4．

    点评 本题主要考查二次函数的解析式，分别用a表示出b和c，得出抛物线解析式是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    6．如图，AB∥CD，点P在CD上，且AP⊥BP，∠ABP=25°，则∠APC=65度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

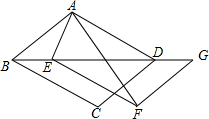    7．如图，在平行四边形ABCD中，∠ABD=30°，AB=4，BD=5$\sqrt{3}$，将△BCD沿方向平移BD，得到△EFG．
    （1）连结AE、DF，求证：四边形AEFD为平行四边形．
    （2）若?AEFD为矩形，求△BCD平移的距离BE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列说法正确的是（　　）
    A．“打开电视机，它正在播《奔跑吧，兄弟》”是必然事件
    B．“一个不透明的袋中装有8个红球，从中摸出一个球是红球”是随机事件
    C．为了了解我市今年夏季家电市场中空调的质量，不宜采用普查的调查方式进行
    D．销售某种品牌的凉鞋，销售商最感兴趣的是该品牌凉鞋的尺码的平均数

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

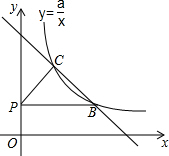    11．如图，在平面直角坐标系中，动点P从原点O开始沿y轴的正方向运动，点B、C是一次 函数y=kx+b与反比例函数y=$\frac{a}{x}$（a＞0，x＞0）的图象的两个交点，且点B（m，2）．当点P的坐标为（0，2）时，PC=BC，且∠PCB=90°．
    （1）试求反比例y=$\frac{a}{x}$（a＞0，x＞0）和一次函数y=kx+b的解析式；
    （2）设a=|PB-PC|，当点P运动到何处时，m的值最大？最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，将平面直角坐标系的纵轴绕原点顺时针旋转30°，得到夹角为60°的平面坐标系xOy，称之为平面60°角坐标系．类比平面直角坐标系中确定点的坐标的方法，设平面60°角坐标系中有任意一点P，过点P作PA∥y轴，交x轴于点A，A点的坐标为（x，0），过点P作PB∥x轴，交y轴于点B，B点的坐标为（0，y），则点P坐标为（x，y）．
    利用以上规定，在平面60°角坐标系中解决下列问题：
    （1）在图12中，过点A（1，0）、B（0，1）分别作y轴、x轴的平行线，两条直线交于点C，则点C的坐标为（1、1）；
    （2）若点M在第二象限，且M到x轴、y轴的距离均为$\sqrt{3}$，则M点坐标为（-2、2）；
    （3）一次函数的图象在平面60°角坐标系中仍然是一条直线，求直线y=x、直线y=-$\frac{1}{2}$x+$\frac{3}{2}$及x轴围成的三角形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

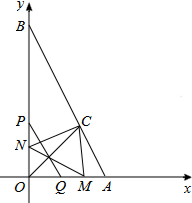    8．如图，已知点A（2，0），B（0，4），∠AOB的角平分线交AB于C，一动点P从O点出发，以每秒2个单位长度的速度，沿y轴向点B作匀速运动，过点P且平行于AB的直线交x轴于Q，作P，Q关于直线OC的对称点M，N．设P运动的时间为t（0＜t＜2）秒
    （1）求出点M，N的坐标（用含t的代数式表示）；
    （2）设△MNC与△OAB重叠部分的面积为S，求关于t的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

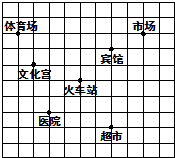    5． 如图，已知火车站的坐标为（2，1），文化宫的坐标为（-1，2）．
    （1）请你根据题目条件，画出平面直角坐标系；
    （2）写出体育馆、市场、超市、宾馆的坐标；
    （3）请将原点O，宾馆C和文化宫B，看作三点用线段连起来，将得△OBC，然后将此三角形向下平移3个单位长度，画出平移后的△O1B1C1，并求出其面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

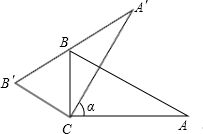    6．直角三角板ABC中，∠A=30°，BC=2．将其绕直角顶点C逆时针旋转一个角α（0°＜α＜120°且α≠90°），得到Rt△A′B′C′
    （1）如图，当A′B′边经过点B时，求旋转角α的度数；
    （2）在三角板旋转的过程中，边A′C′与AB所在直线交于点D，过点 D作DE∥A′B′交CB′边于点E，联结BE．
    ①0°＜α＜90°时，设AD=x，BE=y，求y与x之间的函数解析式及x取值范围；
    ②当${S_{△{B}D{E}}}=\frac{1}{3}{S_{△ABC}}$时，求AD的长．

    查看答案和解析>>

    同步练习册答案