
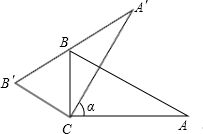
 直角三角板ABC中,∠A=30°,BC=2.将其绕直角顶点C逆时针旋转一个角α(0°<α<120°且α≠90°),得到Rt△A′B′C′
直角三角板ABC中,∠A=30°,BC=2.将其绕直角顶点C逆时针旋转一个角α(0°<α<120°且α≠90°),得到Rt△A′B′C′分析 (1)由旋转的性质可得出∠α=∠B′CB=60°;
(2)①当0°<α<90°时,点D在AB边上(如图).根据平行线DE∥A'B'分线段成比例知$\frac{CD}{CA′}$=$\frac{CE}{CB′}$、及由旋转性质可知,CA=CA',CB=CB',∠ACD=∠BCE由此证明△CAD∽△CBE;根据相似三角形的对应边成比例、直角三角形的性质及∠A=30°求得y=$\frac{\sqrt{3}}{3}$x(0<x<4);
②先求得△ABC的面积,再由△CAD∽△CBE,求得BE,分情况讨论:当点D在AB边上时,AD=x,BD=AB-AD=2-x;当点D在AB的延长线上时,AD=x,BD=x-2.分别列出S△BDE的面积表达式,根据${S_{△{B}D{E}}}=\frac{1}{3}{S_{△ABC}}$列方程解答即可.
解答 解:(1)在Rt△ABC中,∵∠A=30°
∴∠ABC=60°.
由旋转可知:B′C=BC,∠B′=∠ABC=60°,∠α=∠B′CB
∴B′BC为等边三角形.
∠α=∠B′CB60°.
(2)①当0°<α<90°时,点D在AB边上(如图1).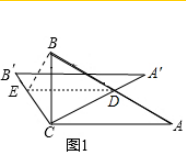
∵DE∥A′B′,
∴$\frac{CD}{CA}$=$\frac{CE}{CB}$.
由旋转性质可知,CA=CA′,CB=CB′,∠ACD=∠BCE.
∴$\frac{CD}{CA}$=$\frac{CE}{CB}$,
∴$\frac{CD}{CE}=\frac{CA}{CB}$,
∴△CAD∽△CBE.
∴$\frac{BE}{AD}$=$\frac{BC}{AC}$.
∵∠A=30°
∴$\frac{y}{x}$=$\frac{BC}{AC}$=$\frac{\sqrt{3}}{3}$.
∴y=$\frac{\sqrt{3}}{3}$x(0<x<4)
②当0°<α<90°时,点D在AB边上.
设AD=x,则BD=AB-AD=4-x,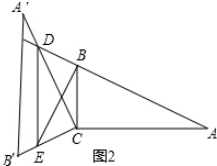
∵DE∥A′B′,
∴$\frac{CD}{CA′}=\frac{CE}{CB′}$,
由旋转性质可知,CA=CA',CB=CB',∠ACD=∠BCE.
∴$\frac{CD}{CA}=\frac{CE}{CB}$,
∴$\frac{CD}{CE}=\frac{CA}{CB}$,
∴△CAD∽△CBE,
∴∠EBC=∠A=30°,又∠CBA=60°,
∴∠DBE=90°.
此时,S△BDE=$\frac{1}{2}$BD×BE=$\frac{1}{2}$(4-x)×$\frac{\sqrt{3}}{3}$x=-$\frac{\sqrt{3}}{6}$x2+$\frac{2\sqrt{3}}{3}$x.
当S=$\frac{1}{3}$S△ABC时,-$\frac{\sqrt{3}}{6}{x}^{2}$+$\frac{2\sqrt{3}}{3}x$=$\frac{2\sqrt{3}}{3}$.
整理,得x2-4x+4=0.
解得x1=x2=2,
即AD=2.
当90°<α<120°时,点D在AB的延长线上(如图2).
设AD=x,则BD=x-4,∠DBE=90°,
此时,S△BDE=$\frac{1}{2}$×BD×BE=$\frac{1}{2}$(x-4)×$\frac{\sqrt{3}}{3}$x=$\frac{\sqrt{3}}{6}$x2-$\frac{2\sqrt{3}}{3}$x,
当S=$\frac{1}{3}$S△ABC时,$\frac{\sqrt{3}}{6}$x2-$\frac{2\sqrt{3}}{3}$x=$\frac{{2\sqrt{3}}}{3}$.
整理,得x2-4x-4=0.
解得x1=2+2$\sqrt{2}$,x2=2-2$\sqrt{2}$(负值,舍去).
即AD=2+2$\sqrt{2}$
综上所述:AD=2或AD=2+2$\sqrt{2}$.
点评 本题主要考查旋转、全等三角形、解直角三角形、平行线分线段成比例等知识.解决本题的关键是结合图形,分类讨论,求出S△BDE的面积表达式是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
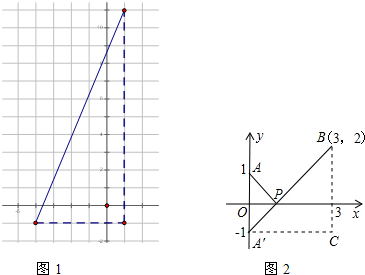
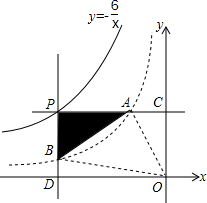 已知点P(a,b)是反比例函数y=-$\frac{6}{x}$(x<0)图象上的动点,PA∥x轴,PB∥y轴,分别交反比例函数y=-$\frac{2}{x}$(x<0)的图象于点A,B,交坐标轴于C,D.
已知点P(a,b)是反比例函数y=-$\frac{6}{x}$(x<0)图象上的动点,PA∥x轴,PB∥y轴,分别交反比例函数y=-$\frac{2}{x}$(x<0)的图象于点A,B,交坐标轴于C,D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
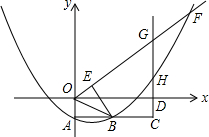 如图,抛物线y=$\frac{1}{2}$x2+mx-n(n>0)与y轴交于点A,过点A作AB∥x轴,交抛物线于点B,延长AB到C,使BC=AB,过点C作CD⊥x轴于点D(4n,0).
如图,抛物线y=$\frac{1}{2}$x2+mx-n(n>0)与y轴交于点A,过点A作AB∥x轴,交抛物线于点B,延长AB到C,使BC=AB,过点C作CD⊥x轴于点D(4n,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
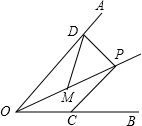 如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )
如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
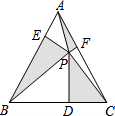 如图,等边△ABC中,P为三角形内一点,过P作PD⊥BC,PE⊥AB,PF⊥AC,连结AP、BP、CP,如果S△APF+S△BPE+S△PCD=$\frac{9\sqrt{3}}{2}$,那么△ABC的内切圆半径为( )
如图,等边△ABC中,P为三角形内一点,过P作PD⊥BC,PE⊥AB,PF⊥AC,连结AP、BP、CP,如果S△APF+S△BPE+S△PCD=$\frac{9\sqrt{3}}{2}$,那么△ABC的内切圆半径为( )| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com