
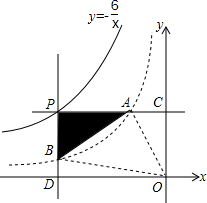
 已知点P(a,b)是反比例函数y=-$\frac{6}{x}$(x<0)图象上的动点,PA∥x轴,PB∥y轴,分别交反比例函数y=-$\frac{2}{x}$(x<0)的图象于点A,B,交坐标轴于C,D.
已知点P(a,b)是反比例函数y=-$\frac{6}{x}$(x<0)图象上的动点,PA∥x轴,PB∥y轴,分别交反比例函数y=-$\frac{2}{x}$(x<0)的图象于点A,B,交坐标轴于C,D.分析 (1)利用点P的坐标可求出S:,S2的值,即可得出S1:S2;
(2)由P(a,b)是反比例函数y=-$\frac{6}{x}$(x<0)图象上的动点,可得P(a,-$\frac{6}{a}$),再由点A、B在反比例函数y=-$\frac{2}{x}$(x<0)即可得出点A、B的坐标;
(3)由S=$\frac{1}{2}$|AP|•|BP|=$\frac{4}{3}$,即可得出S不变化.
解答 解:(1)∵P(a,b)是反比例函数y=-$\frac{6}{x}$(x<0)图象上的动点,
∵P(a,-$\frac{6}{a}$),
∴S1=$\frac{1}{2}$•(-a)•(-$\frac{6}{a}$)=3,
∵B(a,-$\frac{2}{a}$),
∴S2=$\frac{1}{2}$•(-a)•(-$\frac{2}{a}$)=1,
∴S1:S2=3:1=3.
故答案为:3.
(2)∵P(a,b)是反比例函数y=-$\frac{6}{x}$(x<0)图象上的动点,
∵P(a,-$\frac{6}{a}$),
∵点B在反比例函数y=-$\frac{2}{x}$(x<0)上且横坐标为a,
∴B(a,-$\frac{2}{a}$),
∵点A在反比例函数y=-$\frac{2}{x}$(x<0)上且纵坐标为-$\frac{6}{a}$,
∴A($\frac{a}{3}$,-$\frac{6}{a}$),
(3)不变化.
∵P(a,-$\frac{6}{a}$),B(a,-$\frac{2}{a}$),A($\frac{a}{3}$,-$\frac{6}{a}$),PA∥x轴,PB∥y轴,
∴S=$\frac{1}{2}$|AP|•|BP|=$\frac{1}{2}$×($\frac{a}{3}$-a)[(-$\frac{6}{a}$)-(-$\frac{2}{a}$)]=$\frac{4}{3}$.
点评 本题考查了反比例函数的综合知识,题目中根据平行坐标轴的直线上的点的坐标特点表示出有关点的坐标是解答本题的关键,难度中等偏上.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | “打开电视机,它正在播《奔跑吧,兄弟》”是必然事件 | |
| B. | “一个不透明的袋中装有8个红球,从中摸出一个球是红球”是随机事件 | |
| C. | 为了了解我市今年夏季家电市场中空调的质量,不宜采用普查的调查方式进行 | |
| D. | 销售某种品牌的凉鞋,销售商最感兴趣的是该品牌凉鞋的尺码的平均数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
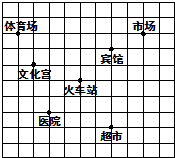 如图,已知火车站的坐标为(2,1),文化宫的坐标为(-1,2).
如图,已知火车站的坐标为(2,1),文化宫的坐标为(-1,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
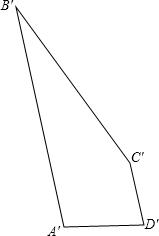 如图所示,四边形A′B′C′D′是将四边形ABCD平移后得到的,已知A′B′=13,B′C′=12,C′D′=3,D′A′=4,求四边形ABCD的周长.
如图所示,四边形A′B′C′D′是将四边形ABCD平移后得到的,已知A′B′=13,B′C′=12,C′D′=3,D′A′=4,求四边形ABCD的周长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
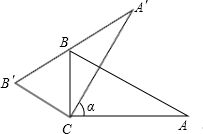 直角三角板ABC中,∠A=30°,BC=2.将其绕直角顶点C逆时针旋转一个角α(0°<α<120°且α≠90°),得到Rt△A′B′C′
直角三角板ABC中,∠A=30°,BC=2.将其绕直角顶点C逆时针旋转一个角α(0°<α<120°且α≠90°),得到Rt△A′B′C′查看答案和解析>>
科目:初中数学 来源: 题型:填空题
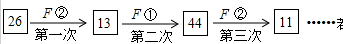
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com