Question

5．已知，在以O为原点的直角坐标系中，抛物线的顶点为A （-1，-4），且经过点B（-2，-3），与x轴分别交于C、D两点．

（1）求直线OB以及该抛物线相应的函数表达式；
（2）如图1，点M是抛物线上的一个动点，且在直线OB的下方，过点M作x轴的平行线与直线OB交于点N，求MN的最大值；
（3）如图2，过点A的直线交x轴于点E，且AE∥y轴，点P是抛物线上A、D之间的一个动点，直线PC、PD与AE分别交于F、G两点．当点P运动时，EF+EG是否为定值？若是，试求出该定值；若不是，请说明理由．

Answer 1

分析 （1）由B点坐标利用待定系数法可求直线OB解析式，利用顶点式可求得抛物线解析式；
（2）设M（t，t²+2t-3），MN=s，则可表示出N点坐标，由MN的纵坐标相等可得到关于s和t的关系式，再利用二次函数的性质可求得其最大值；
（3）设P（t，t²+2t-3），则可表示出PQ、CQ、DQ，再利用相似三角形的性质可用t分别表示出EF和EG的长，则可求得其定值．

解答 解：
（1）设直线OB解析式为y=kx，由题意可得-3=-2k，解得k=$\frac{3}{2}$，
∴直线OB解析式为y=$\frac{3}{2}$x，
∵抛物线顶点坐标为（-1，-4），
∴可设抛物线解析式为y=a（x+1）²-4，
∵抛物线经过B（-2，-3），
∴-3=a-4，解得a=1，
∴抛物线为y=x²+2x-3；
（2）设M（t，t²+2t-3），MN=s，则N的横坐标为t-s，纵坐标为$\frac{3}{2}（t-s）$，
∵MN∥x轴，
∴t²+2t-3=$\frac{3}{2}（t-s）$，得s=$-\frac{2}{3}{t^2}-\frac{1}{3}t+2$=$-\frac{2}{3}{（t+\frac{1}{4}）^2}+\frac{49}{24}$，
∴当t=$-\frac{1}{4}$时，MN有最大值，最大值为$\frac{49}{24}$；
（3）EF+EG=8．
理由如下：
如图2，过点P作PQ∥y轴交x轴于Q，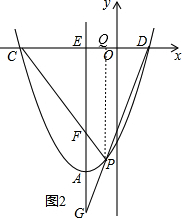

在y=x²+2x-3中，令y=0可得0=x²+2x-3，解得x=-3或x=1，
∴C（-3，0），D（1，0），
设P（t，t²+2t-3），则PQ=-t²-2t+3，CQ=t+3，DQ=1-t，
∵PQ∥EF，
∴△CEF∽△CQP，
∴$\frac{EF}{PQ}$=$\frac{CE}{CQ}$，
∴EF=$\frac{CE}{CQ}$•PQ=$\frac{2}{t+3}$（-t²-2t+3），
同理△EGD∽△QPD得$\frac{EG}{PQ}$=$\frac{DE}{DQ}$，
∴EG=$\frac{DE}{DQ}$•PQ=$\frac{2}{1-t}•（-{t^2}-2t+3）$，
∴EF+EG=$\frac{2}{t+3}$（-t²-2t+3）+$\frac{2}{1-t}•（-{t^2}-2t+3）$=2（-t²-2t+3）（$\frac{1}{t+3}$+$\frac{1}{1-t}$）=2（-t²-2t+3）（$\frac{1-t+t+3}{（t+3）（1-t）}$）=2（-t²-2t+3）（$\frac{4}{{-{t^2}-2t+3}}$）=8，
∴当点P运动时，EF+EG为定值8．

点评 本题为二次函数的综合应用，涉及待定系数法、二次函数的最值、相似三角形的判定和性质及方程思想等知识点．在（1）中注意待定系数的应用步骤，在（2）中利用M、N的纵坐标相等是解题的关键，在（3）中用P点坐标表示出EF和EG的长是解题的关键．本题考查知识点较多，综合性较强，难度较大．