
【题目】如图,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() .以
.以![]() 为直角边且在
为直角边且在![]() 的上方作等腰直角三角形
的上方作等腰直角三角形![]() .
.
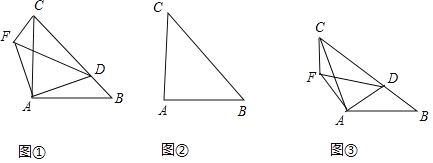
(1)若![]() ,
,![]()
①当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),试探讨
不重合),试探讨![]() 与
与![]() 的数量关系和位置关系;
的数量关系和位置关系;
②当点![]() 在线段
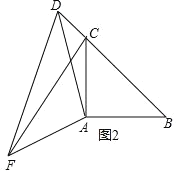
在线段![]() 的延长线上时,①中的结论是否仍然成立,请在图2中面出相应的图形并说明理由;
的延长线上时,①中的结论是否仍然成立,请在图2中面出相应的图形并说明理由;
(2)如图3,若![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动,试探究
上运动,试探究![]() 与
与![]() 的位置关系.
的位置关系.
【答案】(1)①CF⊥BD,证明见解析;②成立,理由见解析;(2)CF⊥BD,证明见解析.
【解析】
(1)①根据同角的余角相等求出∠CAF=∠BAD,然后利用“边角边”证明△ACF和△ABD全等,②先求出∠CAF=∠BAD,然后与①的思路相同求解即可;
(2)过点A作AE⊥AC交BC于E,可得△ACE是等腰直角三角形,根据等腰直角三角形的性质可得AC=AE,∠AED=45°,再根据同角的余角相等求出∠CAF=∠EAD,然后利用“边角边”证明△ACF和△AED全等,根据全等三角形对应角相等可得∠ACF=∠AED,然后求出∠BCF=90°,从而得到CF⊥BD.
解:(1)①∵∠BAC=90°,△ADF是等腰直角三角形,
∴∠CAF+∠CAD=90°,∠BAD+∠ACD=90°,
∴∠CAF=∠BAD,
在△ACF和△ABD中,
∵AB=AC,∠CAF=∠BAD,AD=AF,
∴△ACF≌△ABD(SAS),
∴CF=BD,∠ACF=∠ABD=45°,
∵∠ACB=45°,
∴∠FCB=90°,
∴CF⊥BD;
②成立,理由如下:如图2:
∵∠CAB=∠DAF=90°,
∴∠CAB+∠CAD=∠DAF+∠CAD,
即∠CAF=∠BAD,
在△ACF和△ABD中,
∵AB=AC,∠CAF=∠BAD,AD=AF,
∴△ACF≌△ABD(SAS),
∴CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∴∠BCF=∠ACF+∠ACB=45°+45°=90°,
∴CF⊥BD;
(2)如图3,过点A作AE⊥AC交BC于E,
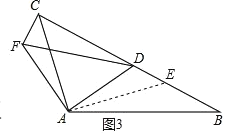
∵∠BCA=45°,
∴△ACE是等腰直角三角形,
∴AC=AE,∠AED=45°,
∵∠CAF+∠CAD=90°,∠EAD+∠CAD=90°,
∴∠CAF=∠EAD,
在△ACF和△AED中,
∵AC=AE,∠CAF=∠EAD,AD=AF,
∴△ACF≌△AED(SAS),
∴∠ACF=∠AED=45°,
∴∠BCF=∠ACF+∠BCA=45°+45°=90°,
∴CF⊥BD.


科目:初中数学 来源: 题型:
【题目】如图,形如量角器的半圆![]() 的直径
的直径![]() ,形如三角板的
,形如三角板的![]() 中,
中,![]() ,
,![]() ,
,![]() ,半圆
,半圆![]() 以
以![]() 的速度从左向右运动,在运动过程中,点
的速度从左向右运动,在运动过程中,点![]() 、
、![]() 始终在直线
始终在直线![]() 上,设运动时间为
上,设运动时间为![]() ,当
,当![]() 时,半圆
时,半圆![]() 在
在![]() 的左侧,
的左侧,![]() .
.
![]() 当
当![]() 时,点
时,点![]() 在半圆
在半圆![]() ________,当
________,当![]() 时,点
时,点![]() 在半圆
在半圆![]() ________;
________;
![]() 当
当![]() 为何值时,
为何值时,![]() 的边
的边![]() 与半圆
与半圆![]() 相切?
相切?
![]() 当
当![]() 为何值时,
为何值时,![]() 的边
的边![]() 与半圆
与半圆![]() 相切?
相切?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c 如图所示,直线x=-1是其对称轴,

(1)确定a,b,c, Δ=b2-4ac的符号,
(2)求证:a-b+c>0,
(3)当x取何值时,y>0;当x取何值时y<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传“扫黑除恶”专项行动,社区准备制作一幅宣传版面,喷绘时为了美观,要在矩形图案四周外围增加一圈等宽的白边,已知图案的长为2米,宽为1米,图案面积占整幅宣传版面面积的90%,若设白边的宽为x米,则根据题意可列出方程( )

A. 90%×(2+x)(1+x)=2×1 B. 90%×(2+2x)(1+2x)=2×1
C. 90%×(2﹣2x)(1﹣2x)=2×1 D. (2+2x)(1+2x)=2×1×90%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 m,n 相交于 O,所夹的锐角是 53°,点 P,Q 分别是直线 m,n上的点,将直线 m,n 按照下面的程序操作,能使两直线平行的是( )

A. 将直线 m 以点 O 为中心,顺时针旋转 53° B. 将直线 n 以点 Q 为中心,顺时针旋转 53°
C. 将直线 m 以点 P 为中心,顺时针旋转 53° D. 将直线 m 以点 P 为中心,顺时针旋转 127°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B是反比例函数y=![]() 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
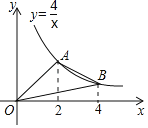
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com