
分析 (1)设一次函数为y=kx+b,把A、B两点坐标代入,解方程组即可.
(2)由题意可以设一次函数为y=3x+b,把(5,3)代入即可.
(3)根据“左加右减,上加下减”的规律写出函数解析式即可.
解答 解:(1)设一次函数为y=kx+b,
把A(1,1)和点B(2,-1)代入得$\left\{\begin{array}{l}{k+b=1}\\{2k+b=-1}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=-2}\\{b=3}\end{array}\right.$,
∴函数解析式为y=-2x+3.
(2)由题意可以设一次函数为y=3x+b,把(5,3)代入得b=-4,
故一次函数解析式为y=3x-4.
(3)将直线y=-2x-1的图象先向左平移2个单位长度,再向上平移1个单位长度得到直线y=-2(x+2)+1,即y=-2x-3.
点评 本题考查待定系数法确定函数解析式,掌握两直线平行k相同,掌握“左加右减,上加下减”直线平移的规律,属于基础题,中考常考题型.


科目:初中数学 来源: 题型:填空题
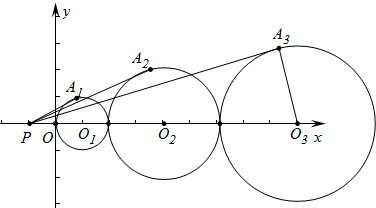 如图,点P(-1,0),以圆心在x轴正半轴上连续作圆,半径分别为1、2、3,过点P作圆的切线,切点分别为A1、A2、A3,则sin∠O3PA3=$\frac{3}{10}$.
如图,点P(-1,0),以圆心在x轴正半轴上连续作圆,半径分别为1、2、3,过点P作圆的切线,切点分别为A1、A2、A3,则sin∠O3PA3=$\frac{3}{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
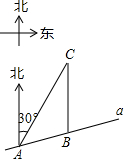 如图,某市郊外景区内一条笔直的公路a经过A、B两个景点,景区管委会又开发了风景优美的景点C,经测量,B位于A的北偏东75°方向,C位于B的正北方向,C位于A的北偏东30°方向,AB=8km.
如图,某市郊外景区内一条笔直的公路a经过A、B两个景点,景区管委会又开发了风景优美的景点C,经测量,B位于A的北偏东75°方向,C位于B的正北方向,C位于A的北偏东30°方向,AB=8km.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
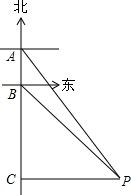 有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是7海里.(结果取整数)(参考数据:$\sqrt{3}$≈1.73)
有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是7海里.(结果取整数)(参考数据:$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
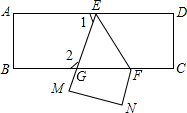 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在MN的位置上,若∠EFG=55°,则∠2=( )
把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在MN的位置上,若∠EFG=55°,则∠2=( )| A. | 105 | B. | 110 | C. | 95 | D. | 120 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
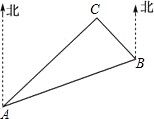 如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )
如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )| A. | 90° | B. | 80° | C. | 70° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com