
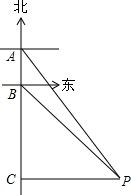
 有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是7海里.(结果取整数)(参考数据:$\sqrt{3}$≈1.73)
有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是7海里.(结果取整数)(参考数据:$\sqrt{3}$≈1.73) 科目:初中数学 来源: 题型:解答题
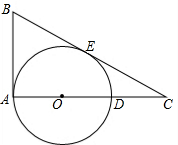 如图,在Rt△ABC中,∠BAC=90°,点O在AC上,BC切⊙O于点E,且AB=5,AC=12.
如图,在Rt△ABC中,∠BAC=90°,点O在AC上,BC切⊙O于点E,且AB=5,AC=12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
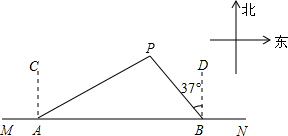 如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东62°方向上,在船B的北偏西37°方向上,若AP=30海里.求船B到船P的距离PB(结果用含非特殊角的三角函数表示即可).
如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东62°方向上,在船B的北偏西37°方向上,若AP=30海里.求船B到船P的距离PB(结果用含非特殊角的三角函数表示即可).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
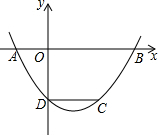 如图,抛物线y=ax2-4ax+c(a、c为常数)与x轴交于点A、B,与y轴交于点D,CD∥x轴.与抛物线交于点C,若点A的坐标为(-1,0).则线段OB与线段CD的长度的和为9.
如图,抛物线y=ax2-4ax+c(a、c为常数)与x轴交于点A、B,与y轴交于点D,CD∥x轴.与抛物线交于点C,若点A的坐标为(-1,0).则线段OB与线段CD的长度的和为9.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com