练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．下列各图中，能够由∠1=∠2得到AB∥CD的是（　　）
    A．B．C．D．

    分析 根据对等角相等可得∠1=∠3，再由∠1=∠2，可得∠3=∠2，根据同位角相等，两直线平行可得AB∥CD．

    解答 解：∵∠1=∠3，∠1=∠2，
    ∴∠3=∠2，
    ∴AB∥CD，
    故选：B．

    点评 此题主要考查了平行线的判定，关键是掌握平行线的判定定理．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    5．利用二次函数y=x2-2x-2的图象求一元二次方程y=x2-2x-2的近似解时，画图如图1示并进一步估算其中一根列表如下，根据这些信息，可得方程的正的近似根是（　　）
    x-0.9-0.8-0.7-0.6
    y=x2-2x-2-0.610.24-0.11-0.44
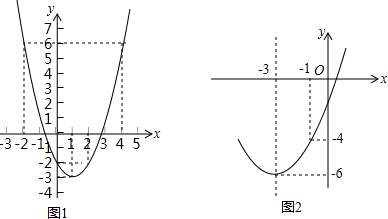
    A．0.7B．2.6C．2.7D．2.8

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

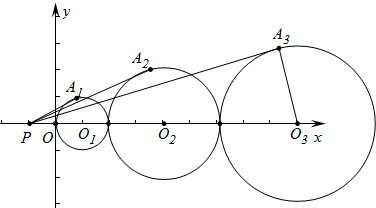    4．如图，点P（-1，0），以圆心在x轴正半轴上连续作圆，半径分别为1、2、3，过点P作圆的切线，切点分别为A1、A2、A3，则sin∠O3PA3=$\frac{3}{10}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

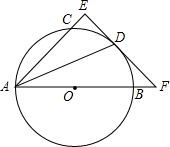    1．如图，AB是圆O的直径，点C、D在圆O上，且AD平分∠CAB．过点D作AC的垂线，与AC的延长线相交于E，与AB的延长线相交于点F．
    求证：EF与圆O相切．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

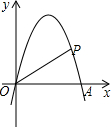    8．如图，在平面直角坐标系中，抛物线y=-x2+4x与x轴交于点O、A，点P在抛物线上，连结OP、AP，设点P的横坐标为m，△AOP的面积为S，若0＜m＜3，则S的取值范围是0＜S≤8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

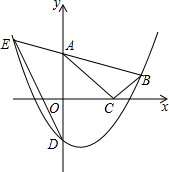    17．如图，在平面直角坐标系中，Rt△ABC的顶点A、C分别在y轴、x轴上，∠ACB=90°，OA=$\sqrt{3}$，抛物线y=ax2-ax-a经过点B（2，$\frac{\sqrt{3}}{3}$），与y轴交于点D．
    （1）求抛物线的表达式；
    （2）点B关于直线AC的对称点是否在抛物线上？请说明理由；
    （3）延长BA交抛物线于点E，连结ED，试说明ED∥AC的理由；
    （4）点P从点O开始沿OC运动，到点C停止，连结AP，过点B作BF⊥AP于F，请直接写出点F的运动路径长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

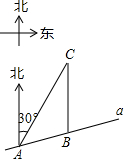    3．如图，某市郊外景区内一条笔直的公路a经过A、B两个景点，景区管委会又开发了风景优美的景点C，经测量，B位于A的北偏东75°方向，C位于B的正北方向，C位于A的北偏东30°方向，AB=8km．
    （1）求景点B与C的距离；
    （2）为方便游客到景点游玩，景区管委会准备由景点C向公路a修一条距离最短的公路，不考虑其它因素，求出这条公路的长．（本题结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

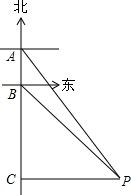    19．有一轮船在A处测得南偏东30°方向上有一小岛P，轮船沿正南方向航行至B处，测得小岛P在南偏东45°方向上，按原方向再航行10海里至C处，测得小岛P在正东方向上，则A，B之间的距离是7海里．（结果取整数）（参考数据：$\sqrt{3}$≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．计算下列各题：
    （1）（2x2）3-6x3（x3+2x2-x）；
    （2）20160-2-2-（-$\frac{1}{2}$）2；
    （3）先化简，再求值：
    [（2a+3b）2-（2a-b）（2a+b）]÷（2b），其中a=-$\frac{1}{2}$，b=-2．

    查看答案和解析>>

    同步练习册答案