
【题目】某小区为了改善居住环境,准备修建一个巨型花园ABCD,为了节约材料并种植不同花卉,决定花园一边靠墙,三边用栅栏围住,中间用一段垂直于墙的栅栏隔成两块.已知所用栅栏的总长为60米,墙长为30米,设花园垂直于墙的一边的长为![]() 米.
米.

(1)若平行于墙的一边长为![]() 米,直接写出
米,直接写出![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,这个矩形花园的面积最大?最大值为多少?(栅栏占地面积忽略不计)
为何值时,这个矩形花园的面积最大?最大值为多少?(栅栏占地面积忽略不计)
(3)当这个花园的面积不小于288平方米时,试结合函数图象,直接写出![]() 的取值范围
的取值范围
【答案】(1)y= -3x+60(10≤x<20);(2)当x=10时花园面积最大,为300平方米;(3)10≤x≤12
【解析】
(1)由题意可知栅栏的总长60米可以看做有BC,AB,CD和EF四段组成,把已知数据代入即可求出y和x的函数关系;
(2)利用矩形的面积公式:长×宽和(1)的结论即可得到S和x的关系式,再利用二次函数的性质即可求出当x为何值时,这个矩形花园的面积最大和其最大值;
(3)由(2)可知函数的关系式,由此关系式画出函数的图象,结合图象可直接写出x的取值范围.
解:如图:
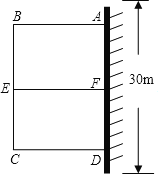
(1)∵AB+CD+EF+BC=60,AB=EF=CD=x,BC=y,
∴3x+y=60,
∴y=-3x+60(10≤x<20);
(2)∵S=xy=x(-3x+60),
∴S=-3x2+60x,
∵a=-3<0,
∴当x=![]() 时,S有最大值
时,S有最大值![]() =300平方米;
=300平方米;
(3)∵这个花园的面积不小288平方米,
∴-3x2+60x≥288,
∴-3x2+60x-288≥0.
设y=-3x2+60x-288≥0.
此函数的图象如图所示:
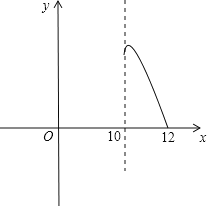
∴当这个花园的面积不小288平方米时,出x的取值范围是:10≤x≤12.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,∠E=30°,AC=5.
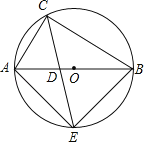
(1)求CE的长;
(2)求S△ADC:S△ACE的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
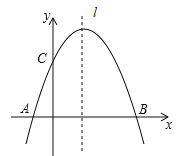
【题目】已知抛物线![]() 经过A(-1,0)、B(3,0)点,直线l是抛物线的对称轴.
经过A(-1,0)、B(3,0)点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)在直线l上确定一点P,使△PAC的周长最小,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
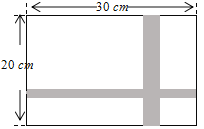
【题目】如图,要设计一副宽20 cm、长30 cm的图案,其中有一横一竖的彩条,横、竖彩条的宽度之比为2∶3.如果要彩条所占面积是图案面积的19%,问横、竖彩条的宽度各为多少cm?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形![]() 中,
中,![]() 厘米,
厘米,![]() 厘米(
厘米(![]() ).动点
).动点![]() 同时从
同时从![]() 点出发,分别沿
点出发,分别沿![]() ,
,![]() 运动,速度是
运动,速度是![]() 厘米/秒.过
厘米/秒.过![]() 作直线垂直于
作直线垂直于![]() ,分别交
,分别交![]() ,
,![]() 于
于![]() .当点
.当点![]() 到达终点
到达终点![]() 时,点
时,点![]() 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为![]() 秒.
秒.
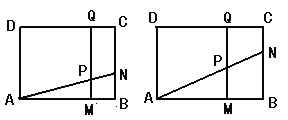
(1)若![]() 厘米,
厘米,![]() 秒,求PM的长度;
秒,求PM的长度;
(2)若![]() 厘米,求出某个时间
厘米,求出某个时间![]() ,使⊿PNB∽⊿PAD,并求出它们的相似比;
,使⊿PNB∽⊿PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
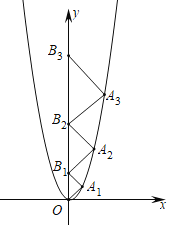
【题目】二次函数y=2x2的图象如图所示,坐标原点O,点B1,B2,B3在y轴的正半轴上,点A1,A2,A3在二次函数y=2x2位于第一象限的图象上,若△A1OB1,△A2B1B2,△A3B2B3都为等腰直角三角形,且点A1,A2,A3均为直角顶点,则点A3的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com