
����Ŀ�������������������ϳ����������Ѽ�ˮ��������760Ԫ�����ס�������Ʒ�ֵ����ϣ������깲����360Ԫ������ۺ��ۼ������
��Ʒ�� | ��Ʒ�� | |
���ۣ�Ԫ/ǧ�ˣ� | 1.6 | 1.4 |
�ۼۣ�Ԫ/ǧ�ˣ� | 2.4 | 2 |
��1����Ѽ�ˮ�����й����ס�������Ʒ�ֵ����ϸ�����ǧ�ˣ�
��2���������۽Ϻã��ó��о������������ٹ����ף�������Ʒ�����ϣ�������Ʒ�����ϵ��������䣬������Ʒ�����ϵ�������ԭ����2������Ʒ�����ϰ�ԭ�����ۣ���Ʒ�������������ۣ�������Ʒ�ֵ������������������560Ԫ������Ʒ����������ۼ�Ϊ����Ԫ��
���𰸡���1��300ǧ�ˣ� 200ǧ��;��2��1.8Ԫ/ǧ�ˣ�
��������
��1����Ѽ�ˮ�����й�����Ʒ������xǧ�ˣ�������Ʒ������yǧ�ˣ������ܼ�=�������������������=ÿǧ�˵����������������ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
��2������Ʒ�����ϵ��ۼ�ΪmԪ/ǧ�ˣ�����������=ÿǧ�˵���������������������������560Ԫ�����ɵó�����m��һԪһ�β���ʽ����֮ȡ���е���Сֵ���ɵó����ۣ�
�⣺��1����Ѽ�ˮ�����й�����Ʒ������xǧ�ˣ�������Ʒ������yǧ�ˣ�
�����⣬�ã�![]() ��
��
��ã�![]() ��
��
�𣺼Ѽ�ˮ�����й�����Ʒ������300ǧ�ˣ�������Ʒ������200ǧ�ˣ�
��2������Ʒ�����ϵ��ۼ�ΪmԪ/ǧ�ˣ�
�����⣬�ã�300��2����2.4��1.6��+200����m��1.4����560��
��ã�m��1.8��
����Ʒ����������ۼ�Ϊ1.8Ԫ/ǧ�ˣ�


 �żӾ���ϵ�д�
�żӾ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
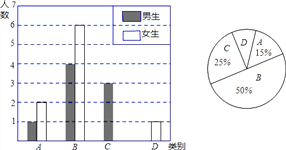
����Ŀ������ʵʩ�¿γ̸ĸ��ѧ��������ѧϰ���������������кܴ���ߣ�����ʦΪ���˽�༶ѧ������ѧϰ�����������ľ����������ij�ಿ��ѧ��������Ϊ�ڰ���µĸ��ٵ��飬�����������ֳ����࣬A���ر�ã�B���ã�C��һ�㣻D���ϲ�������������Ƴ�����������������ͳ��ͼ���������ͳ��ͼ����������⣺
��1�����ε����У�����ʦһ���������� ��ͬѧ������Ů�������� ___����
��2�������������ͳ��ͼ����������
��3��Ϊ�˹�ͬ����������ʦ��ӱ������A���D��ѧ���зֱ�ѡȡһλͬѧ������һ��һ������ѧϰ�������б���������ͼ�ķ��������ѡ��λͬѧǡ����һλ��ͬѧ��һλŮͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() ��ֱ��
��ֱ��![]() ��
��![]() ����
����![]() ��Գƣ���
��Գƣ���![]() ���ڵ�
���ڵ�![]() ��
��
��1����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2������![]() ��
��![]() ����ֱ��
����ֱ��![]() ����
����![]() ����
����![]() �ڵ�
�ڵ�![]() ,��
,��![]() ����
����![]() �ڵ�
�ڵ� ![]() ����֤��
����֤��![]()
��3����ͼ2�����![]() ��
��![]() ������ƽ�ƣ�
������ƽ�ƣ�![]() �߽�
�߽�![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ���ӳ����ϵ�һ�㣬��
���ӳ����ϵ�һ�㣬��![]() ��
��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ƽ�ƵĹ����У�
ƽ�ƵĹ����У�![]() �ij����Ƿ�Ϊ��ֵ����˵�����ɣ�
�ij����Ƿ�Ϊ��ֵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʾ���߳�Ϊa������������һ���߳�Ϊb��С�����Σ���ͼ2��ʾ����ͼ1����Ӱ����ƴ�ɵ�һ�������Σ�
��1����ͼ1����Ӱ�������ΪS1��ͼ2����Ӱ�������ΪS2����ֱ���ú�a��b�Ĵ���ʽ��ʾS1��S2��
��2����д��������������ʾ�ij˷���ʽ��
��3�������������ʽ���㣺��2+1����22+1����24+1����28+1��+1��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������䷢���к�����й©����й©��ʼ����ȫ����������![]() ��֮��й©���к�������д������߶�
��֮��й©���к�������д������߶�![]() ��ʾ����й©ʱ�����ڼ�����ʾ����
��ʾ����й©ʱ�����ڼ�����ʾ����![]() ��ʱ��
��ʱ��![]() (
(![]() ) ֮��ĺ�����ϵ(
) ֮��ĺ�����ϵ(![]() )�� ����������
)�� ����������![]() ��Ӧ����
��Ӧ����![]() ��ʾ����й©���ƺ������ʾ����
��ʾ����й©���ƺ������ʾ����![]() ��ʱ��
��ʱ��![]() (
(![]() ) ֮��ĺ�����ϵ(
) ֮��ĺ�����ϵ(![]() ).����ͼ������������:
).����ͼ������������:
(1)���������������й©֮����ʾ������(����![]() ��������)��
��������)��
(2)��������![]() �ı���ʽ�� ��ȷ�������ڼ����ָ�������й©֮������ʱ��Ӧ
�ı���ʽ�� ��ȷ�������ڼ����ָ�������й©֮������ʱ��Ӧ![]() ��ֵ.
��ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
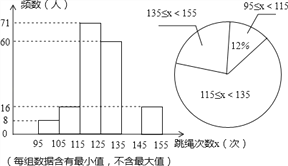
����Ŀ�������п�չ�ġ�����������������У�Ϊ���˽���ѧ��������Ŀ�չ�������������ȫ�а��꼶����ͬѧ1���������Ĵ����������������ͳ�ƣ�������������������ͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺
��1�����ι�����˶�����ѧ����
��2���벹ȫƵ���ֲ�ֱ��ͼ��ȱ���֣�ֱ��д������ͳ��ͼ������������Χ135��x��155�������ε�Բ�ĽǶ�����
��3�������γ���У�����������125�����ϣ���125�Σ�Ϊ���㣬�������ȫ��8000�����꼶ѧ�����ж�����ѧ���ijɼ�Ϊ���㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��ֱ��ѹס����OB����һ��ֱ��ѹס����OA�������һ��ֱ�߽��ڵ�P��С��˵��������OP���ǡ�BOA�Ľ�ƽ���ߣ������������������ǣ� ��
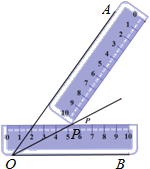
A.��ƽ�����ϵĵ㵽��������ߵľ������
B.�ǵ��ڲ����ǵ����ߵľ�����ȵĵ��ڽǵ�ƽ������
C.������������ƽ���ߵĽ��㵽�����ߵľ������
D.���Ͼ�����ȷ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ڡ�ABC�У�D��AB���е㣬�ҡ�ACD=��B���� AB=10����AC�ij���
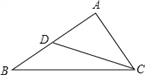
���𰸡�5![]() .
.
�����������������
�ɵ�D��AB���е㣬AB=10����AD=5�����ɡ�ACD=��B����A=��A����֤����
��ACD�ס�ABC���Ӷ��ɵã� ![]() ���ɴ˵õ���AC2=AD
���ɴ˵õ���AC2=AD![]() AB=50���ɽ��AC��ֵ.
AB=50���ɽ��AC��ֵ.
���������
�ߡ�ACD=��B����A=��A��
���ACD�ס�ABC��
��![]() ��
��
��AC2=AD![]() AB.
AB.
��D��AB���е㣬AB=10��
��AD=![]() AB=5,
AB=5,
��AC2=50��
���AC=![]() .
.
�����͡������
��������
22
����Ŀ���ڴ���װ���ĸ���С��ȫ��ͬ��С�����Ƿֱ���1,2,3,4�������������һ���������ֺ�Żأ��ٴ����������һ����������״ͼ���߱����������������С�����͵���4�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��x�ύ�ڵ�A��B����y�ύ�ڵ�C����OΪ����ԭ�㣬��DΪ�����߶��㣬��E���������ϣ���F��x���ϣ��ı���OCEFΪ���Σ���OF=2��EF=3
��x�ύ�ڵ�A��B����y�ύ�ڵ�C����OΪ����ԭ�㣬��DΪ�����߶��㣬��E���������ϣ���F��x���ϣ��ı���OCEFΪ���Σ���OF=2��EF=3
��1��������������Ӧ�ĺ�������ʽ��
��2������ABC�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com