
【题目】学习全等三角形的判定方法以后,我们知道“已知两边和一角分别相等的两个三角形不一定全等”,但下列两种情形还是成立的.
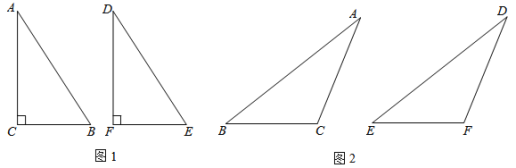
(1)第一情形(如图1)在△ABC和△DEF中,∠C=∠F=90°,AC=DF,AB=DE,则根据__________,得出△ABC≌△DEF;
(2)第二情形(如图2)在△ABC和△DEF中,∠C=∠F(∠C和∠F均为钝角),AC=DF,AB=DE,求证:△ABC≌△DEF.
【答案】(1)HL;(2)证明见解析.
【解析】
(1)根据直角三角形全等的判定方法HL,可证明△ABC≌△DEF,可得出答案;
(2)可过A作AG⊥BC,交BC的延长线于点G,D点作DH⊥EF,交EF的延长线于点H,可先证明△ACG≌△DFH,可得到AG=DH,再证明△ABG≌△DEH,可得∠B=∠E,可证得结论.
(1)解:AC、DF为直角边,AB、DE为斜边,且∠C=∠F=90°,
故可根据“HL”可证明△ABC≌△DEF,
故答案为:HL;
(2)证明:如图,过A作AG⊥BC,交BC的延长线于点G,D点作DH⊥EF,交EF的延长线于点H,
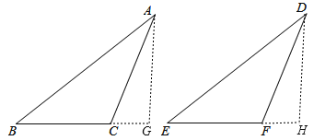
∵∠BCA=∠EFD,
∴∠ACG=∠DFH,
在△ACG和△DFH中,
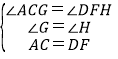 ,
,
∴△ACG≌△DFH(AAS),
∴AG=DH,
在Rt△ABG和Rt△DEH中,
![]() ,
,
∴△ABG≌△DEH(HL),
∴∠B=∠E,
在△ABC和△DEF中,
 ,
,
∴△ABC≌△DEF(AAS).


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】如图, ![]() 是
是 ![]() 的中线,
的中线, ![]() 是线段
是线段 ![]() 上一点(不与点
上一点(不与点 ![]() 重合).
重合). ![]() 交
交 ![]() 于点
于点 ![]() ,
, ![]() ,连结
,连结 ![]() .
.
(1)如图1,当点 ![]() 与
与 ![]() 重合时,求证:四边形
重合时,求证:四边形 ![]() 是平行四边形;
是平行四边形;
(2)如图2,当点 ![]() 不与
不与 ![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长 ![]() 交
交 ![]() 于点
于点 ![]() ,若
,若 ![]() ,且
,且 ![]() .当
.当 ![]() ,
, ![]() 时,求
时,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了顺利通过“国家文明城市”验收,市政府拟对部分路段的人行道地砖、绿化带、排水管等公用设施全面更新改造,根据市政建设的需要,需在40天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的费用是4.5万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完成工程,又能使工程费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.DE=6cm,AD=9cm,则BE的长是( )
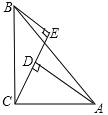
A. 6cm B. 1.5cm C. 3cm D. 4.5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):
选项 | 频数 | 频率 |
A | 10 | m |
B | n | 0.2 |
C | 5 | 0.1 |
D | p | 0.4 |
E | 5 | 0.1 |
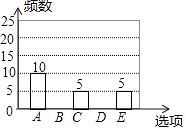
根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调查结果,就中学生如何合理使用手机给出你的一条建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
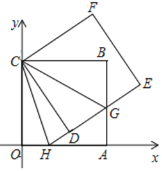
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连结CH、CG.
(1)求证:CG平分∠DCB;
(2)在正方形ABCO绕点C逆时针旋转的过程中,求线段HG、OH、BG之间的数量关系;
(3)连结BD、DA、AE、EB,在旋转的过程中,四边形AEBD是否能在点G满足一定的条件下成为矩形?若能,试求出直线DE的解析式;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,射线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF。
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com