练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如下图所示，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D．DE=6cm，AD=9cm，则BE的长是（ ）

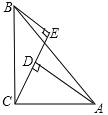
    A. 6cm B. 1.5cm C. 3cm D. 4.5cm

    【答案】C

    【解析】

    本题可通过全等三角形来求BE的长．△BEC和△CDA中，已知了一组直角，∠CBE和∠ACD同为∠BCE的余角，AC=BC，可据此判定两三角形全等；那么可得出的条件为CE=AD，BE=CD，因此只需求出CD的长即可．而CD的长可根据CE即AD的长和DE的长得出，由此可得解．

    解：∵∠ACB=90°，BE⊥CE，

    ∴∠BCE+∠ACD=90°，∠BCE+∠CBE=90°；

    ∴∠ACD=∠CBE，又AC=BC，

    ∴△ACD≌△CBE；

    ∴EC=AD，BE=DC；

    ∵DE=6cm，AD=9cm，则BE的长是3cm．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

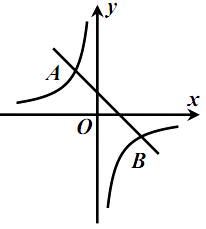
    【题目】如图，一次函数 （ ）与反比例函数 （ ）的图象交于点 ， ．

    （1）求这两个函数的表达式；
    （2）在 轴上是否存在点 ，使 为等腰三角形？若存在，求 的值；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，已知在△ABC中，∠C=90°，AC=5，AB=13．点D在边AC上，且点D到边AB和边BC的距离相等．

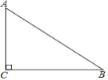
    (1)用直尺圆规作出点D（不写作法，保留作图痕迹，在图上标注清楚点D）；

    (2)求△ABD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在“母亲节”前期，某花店购进康乃馨和玫瑰两种鲜花，销售过程中发现康乃馨比玫瑰销售量大，店主决定将玫瑰每枝降价1元促销，降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍，求降价后每枝玫瑰的售价是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在下列条件中，不能证明△ABD≌△ACD的条件是（ ）

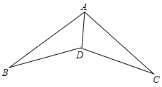
    A. ∠B=∠C，BD=DC B. ∠ADB=∠ADC，BD=DC

    C. ∠B=∠C，∠BAD=∠CAD D. BD=DC，AB=AC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

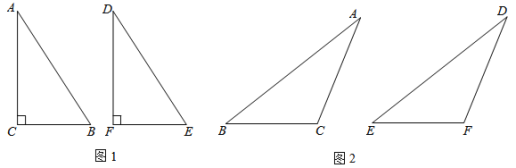
    【题目】学习全等三角形的判定方法以后，我们知道“已知两边和一角分别相等的两个三角形不一定全等”，但下列两种情形还是成立的．

    （1）第一情形（如图1）在△ABC和△DEF中，∠C=∠F=90°，AC=DF，AB=DE，则根据__________，得出△ABC≌△DEF；

    （2）第二情形（如图2）在△ABC和△DEF中，∠C=∠F（∠C和∠F均为钝角），AC=DF，AB=DE，求证：△ABC≌△DEF.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

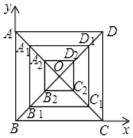
    【题目】如图以正方形ABCD的B点为坐标原点．BC所在直线为x轴，BA所在直线为y轴，建立直角坐标系．设正方形ABCD的边长为6，顺次连接OA、OB、OC、OD的中点A1、B1、C1、D1，得到正方形A1B1C1D1，再顺次连接OA1、OB1、OC1、OD1的中点得到正方形A2B2C2D2．按以上方法依次得到正方形A1B1C1D1，……AnBnCnDn，（n为不小于1的自然数），设An点的坐标为（xn，yn），则xn+yn=______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB，CD，OE⊥AB,过点O画直线MN⊥CD. 若点F是直线MN上任意一点(点O除外)，且∠AOC=34°.求∠EOF的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先化简再求值：（x+2﹣ ）÷（ + ），其中x是不等式组 的整数解．

    查看答案和解析>>

    同步练习册答案