
【题目】如图, ![]() 是
是 ![]() 的中线,
的中线, ![]() 是线段
是线段 ![]() 上一点(不与点
上一点(不与点 ![]() 重合).
重合). ![]() 交
交 ![]() 于点
于点 ![]() ,
, ![]() ,连结
,连结 ![]() .
.
(1)如图1,当点 ![]() 与
与 ![]() 重合时,求证:四边形
重合时,求证:四边形 ![]() 是平行四边形;
是平行四边形;
(2)如图2,当点 ![]() 不与
不与 ![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长 ![]() 交
交 ![]() 于点
于点 ![]() ,若
,若 ![]() ,且
,且 ![]() .当
.当 ![]() ,
, ![]() 时,求
时,求 ![]() 的长.
的长.
【答案】
(1)
证明:∵DE//AB,∴∠EDC=∠ABM,
∵CE//AM,
∴∠ECD=∠ADB,
又∵AM是△ABC的中线,且D与M重合,∴BD=DC,
∴△ABD△EDC,
∴AB=ED,又∵AB//ED,
∴四边形ABDE为平行四边形。
;∵CE//AM,
∴∠ECD=∠ADB,
又∵AM是△ABC的中线,且D与M重合,∴BD=DC,
∴△ABD△EDC,
∴AB=ED,又∵AB//ED,
∴四边形ABDE为平行四边形。
(2)
解:结论成立,理由如下:
过点M作MG//DE交EC于点G,
∵CE//AM,
∴四边形DMGE为平行四边形,
∴ED=GM且ED//GM,
由(1)可得AB=GM且AB//GM,
∴AB=ED且AB//ED.
∴四边形ABDE为平行四边形.
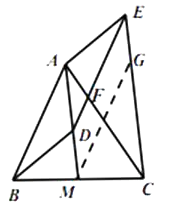
(3)
解:取线段HC的中点I,连结MI,
∴MI是△BHC的中位线,
∴MI//BH,MI=![]() BH,
BH,
又∵BH⊥AC,且BH=AM,
∴MI=![]() AM,MI⊥AC,
AM,MI⊥AC,
∴∠CAM=30°
设DH=x,则AH=![]() x,AD=2x,
x,AD=2x,
∴AM=4+2x,∴BH=4+2x,
由(2)已证四边形ABDE为平行四边形,
∴FD//AB,
∴△HDF~△HBA,
∴![]() , 即
, 即![]()
解得x=1±![]() (负根不合题意,舍去)
(负根不合题意,舍去)
∴DH=1+![]() .
.

;解:取线段HC的中点I,连结MI,
∴MI是△BHC的中位线,
∴MI//BH,MI=![]() BH,
BH,
又∵BH⊥AC,且BH=AM,
∴MI=![]() AM,MI⊥AC,
AM,MI⊥AC,
∴∠CAM=30°
设DH=x,则AH=![]() x,AD=2x,
x,AD=2x,
∴AM=4+2x,∴BH=4+2x,
由(2)已证四边形ABDE为平行四边形,
∴FD//AB,
∴△HDF~△HBA,
∴![]() , 即
, 即![]()
解得x=1±![]() (负根不合题意,舍去)
(负根不合题意,舍去)
∴DH=1+![]() .;
.;
【解析】(1)由DE//AB,可得同位角相等:∠EDC=∠ABM,由CE//AM,可得同位角相等∠ECD=∠ADB,又由BD=DC,则△ABD△EDC,得到AB=ED,根据有一组对边平行且相等,可得四边形ABDE为平行四边形.
(2)过点M作MG//DE交EC于点G,则可得四边形DMGE为平行四边形,且ED=GM且ED//GM,由(1)可得AB=GM且AB//GM,即可证得;
(3)在已知条件中没有已知角的度数时,则在求角度时往特殊角30°,60°,45°的方向考虑,则要求这样的特殊角,就去找边的关系,构造直角三角形,取线段HC的中点I,连结MI,则MI是△BHC的中位线,可得MI//BH,MI=![]() BH,且MI⊥AC,则去找Rt△AMI中边的关系,求出∠CAM;
BH,且MI⊥AC,则去找Rt△AMI中边的关系,求出∠CAM;
设DH=x,即可用x分别表示出AH=![]() x,AD=2x,AM=4+2x,BH=4+2x,由△HDF~△HBA,得到对应边成比例,求出x的值即可;
x,AD=2x,AM=4+2x,BH=4+2x,由△HDF~△HBA,得到对应边成比例,求出x的值即可;
【考点精析】掌握平行四边形的判定与性质是解答本题的根本,需要知道若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案科目:初中数学 来源: 题型:
【题目】某公司要把240吨白砂糖运往某市的A、B两地,用大小两种货车共20辆,恰好能一次性装完这批白砂糖.已知这两种大小货车的载重分别是15吨/辆和10吨/辆,运往A地的运费为:大车630元/辆,小车420元/辆;运往B地的运费为:大车750元/辆,小车550元/辆.
(1)求大小两种货车各多少辆.
(2)如果安排10辆货车前往A地,其中调往A地的大货车有a辆,其余货车前往B地,填写下表:
前往A地 | 前往B地 | |
大货车/辆 | a | |
小货车/辆 |
(3)按照上表的分配方案,若设总费用为W,求W与a的关系式(用含a的代数式表示W)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某专卖店有![]() ,
,![]() 两种商品.已知在打折前,买60件
两种商品.已知在打折前,买60件![]() 商品和30件
商品和30件![]() 商品用了1080元,买50件
商品用了1080元,买50件![]() 商品和10件
商品和10件![]() 商品用了840元;
商品用了840元;![]() ,
,![]() 两种商品打相同折以后,某人买500件
两种商品打相同折以后,某人买500件![]() 商品和450件
商品和450件![]() 商品一共比不打折少花1960元,计算打了多少折?
商品一共比不打折少花1960元,计算打了多少折?
查看答案和解析>>
科目:初中数学 来源: 题型:
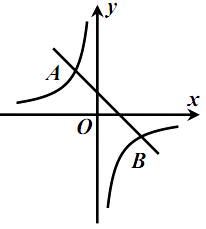
【题目】如图,一次函数 ![]() (
( ![]() )与反比例函数
)与反比例函数 ![]() (
( ![]() )的图象交于点
)的图象交于点 ![]() ,
, ![]() .
.
(1)求这两个函数的表达式;
(2)在 ![]() 轴上是否存在点
轴上是否存在点 ![]()
![]() ,使
,使 ![]() 为等腰三角形?若存在,求
为等腰三角形?若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在七年级下册“证明”的一章的学习中,我们曾做过如下的实验:
画∠AOB=90°,并画∠AOB的平分线OC.
(1)把三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边分别与OA、OB相交于点E、F(如图①).度量PE、PF的长度,这两条线段相等吗?
(2)把三角尺绕点P旋转(如图②),PE与PF相等吗?请说明理由.
(3)探究:画∠AOB=50°,并画∠AOB的平分线OC,在OC上任取一点P,作∠EPF=130°.∠EPF的两边分别与OA、OB相交于E、F两点(如图③),PE与PF相等吗?请说明理由.
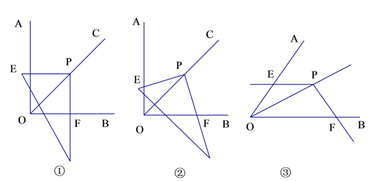
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有__________对,邻补角有__________对.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习全等三角形的判定方法以后,我们知道“已知两边和一角分别相等的两个三角形不一定全等”,但下列两种情形还是成立的.
(1)第一情形(如图1)在△ABC和△DEF中,∠C=∠F=90°,AC=DF,AB=DE,则根据__________,得出△ABC≌△DEF;
(2)第二情形(如图2)在△ABC和△DEF中,∠C=∠F(∠C和∠F均为钝角),AC=DF,AB=DE,求证:△ABC≌△DEF.
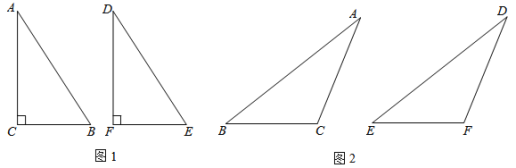
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com