
【题目】在七年级下册“证明”的一章的学习中,我们曾做过如下的实验:
画∠AOB=90°,并画∠AOB的平分线OC.
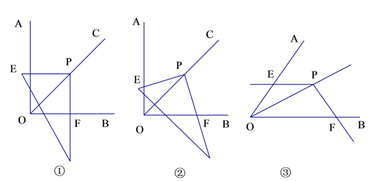
(1)把三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边分别与OA、OB相交于点E、F(如图①).度量PE、PF的长度,这两条线段相等吗?
(2)把三角尺绕点P旋转(如图②),PE与PF相等吗?请说明理由.
(3)探究:画∠AOB=50°,并画∠AOB的平分线OC,在OC上任取一点P,作∠EPF=130°.∠EPF的两边分别与OA、OB相交于E、F两点(如图③),PE与PF相等吗?请说明理由.
【答案】(1)PE=PF;(2)PE=PF;理由见解析;(3)PE=PF;理由见解析
【解析】试题分析:(1)由条件可知PE=PF;
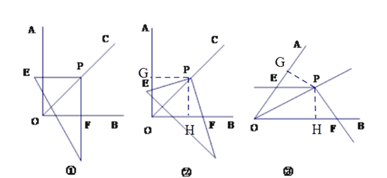
(2)过点P作PG⊥OA,PH⊥OB,垂足是G,H,利用条件证明△PEM≌△PFN即可得出结论;
(3)过点P作PG⊥OA,PH⊥OB,垂足是G,H,利用条件证明△PEM≌△PFN即可得出结论;
试题解析:(1)PE=PF;
(2)PE=PF,理由如下:
过点P作PG⊥OA,PH⊥OB,垂足是G,H,则∠PGE=∠PHF=90°,
∵OP平分∠AOB,∴PG=PH,
∵∠AOB=∠PGE=∠PHF=90°,∴∠GPH=90°,
∵∠EPF=90°,∴∠GPE=∠FPH,
∴△PEG≌△PFH(ASA),
∴PE=PF;
(3)PE=PF,理由如下:
过点P作PG⊥OA,PH⊥OB,垂足是G,H,则∠PGE=∠PHF=90°,
∵OP平分∠AOB,∴PG=PH,
∵∠AOB=50°,∴∠GPH=130°,
∵∠EPF=130°,∴∠GPE=∠FPH,
∴△PEG≌△PFH(ASA),
∴PE=PF;


科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)(﹣3)×(﹣ ![]() )÷(﹣1
)÷(﹣1 ![]() )
)
(2)48×( ![]() )﹣(﹣48)÷(﹣8)
)﹣(﹣48)÷(﹣8)
(3)(﹣1)2013﹣22﹣|﹣ ![]() |×(﹣10)2﹣19
|×(﹣10)2﹣19 ![]() ×19 (用简便方法计算)
×19 (用简便方法计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣5+(﹣0.25)+14﹣(﹣ ![]() );
);
(2)( ![]() +
+ ![]() ﹣1)×(﹣12);
﹣1)×(﹣12);
(3)1 ![]() ÷(﹣
÷(﹣ ![]() )×(
)×( ![]() ﹣4);
﹣4);
(4)2﹣60÷(﹣2)3×(﹣ ![]() )﹣1 .
)﹣1 .
查看答案和解析>>
科目:初中数学 来源: 题型:
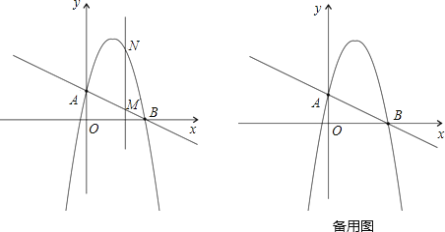
【题目】如图,一次函数y=-![]() x+2分别交y轴、x轴于A、B两点,抛物线y=-
x+2分别交y轴、x轴于A、B两点,抛物线y=-![]() +bx+c过A、B两点.
+bx+c过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列两个命题:①若两个角是对顶角,则这两个角相等;②若一个三角形的两个内角分别为30°和60°,则这个三角形是直角三角形.说法正确的是( )
A.命题①正确,命题②不正确
B.命题①、②都正确
C.命题①不正确,命题②正确
D.命题①、②都不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生动地课外阅读的喜好,某校从八年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其它”类统计,下面是整理数据后绘制的两幅不完整的统计图,以下结论不正确的是( ) 
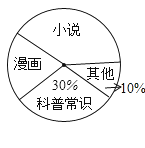
A.由这两个统计图可知喜欢“科学常识”的学生有90人
B.若该年级共有12000名学生,则由这两个统计图可估计喜爱“科学常识”的学生有360人
C.在扇形统计图汇总“漫画”所在扇形的圆心角为72°
D.由这两个统计图不能确定喜欢“小说”的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,正确的个数是( )
①若三条线段的比为1:1:![]() ,则它们组成一个等腰直角三角形;②两条对角线相等的平行四边形是矩形;③对角线互相垂直的四边形是菱形;④1,
,则它们组成一个等腰直角三角形;②两条对角线相等的平行四边形是矩形;③对角线互相垂直的四边形是菱形;④1,![]() ,2是一组勾股数;⑤命题“若两个实数相等,则它们的平方相等”的逆命题成立⑥一次函数
,2是一组勾股数;⑤命题“若两个实数相等,则它们的平方相等”的逆命题成立⑥一次函数![]() =kx+b,若k>0,b<0,那么它的图象过第一、二、三象限;⑦函数y=-6x+3是一次函数,且y随着x的增大而减小;
=kx+b,若k>0,b<0,那么它的图象过第一、二、三象限;⑦函数y=-6x+3是一次函数,且y随着x的增大而减小;
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com