
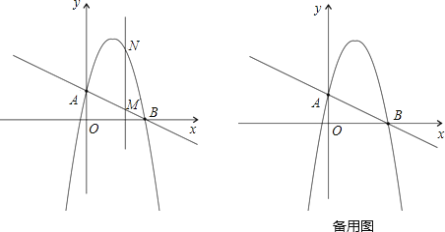
【题目】如图,一次函数y=-![]() x+2分别交y轴、x轴于A、B两点,抛物线y=-
x+2分别交y轴、x轴于A、B两点,抛物线y=-![]() +bx+c过A、B两点.
+bx+c过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
【答案】(1)、y=-![]() +3.5x+2;(2)、t=2时,最大值为4;(3)、(0,6),(0,-2)或(4,4)
+3.5x+2;(2)、t=2时,最大值为4;(3)、(0,6),(0,-2)或(4,4)
【解析】
试题分析:(1)、根据题意得出点A和点B的坐标,然后将两点代入函数解析式得出b和c的值,得出函数解析式;(2)、设出点M和点N的坐标,从而得出MN的长度,根据二次函数的性质得出最大值;(3)、根据题意得出点A、点M和点N的坐标,然后根据平行四边形的性质得出三种情况,从而求出点D的坐标.
试题解析:(1)、求A、B点的坐标为:A(0,2),B(4,0) 将x=0,y=2代入y=-![]() +bx+c得c=2
+bx+c得c=2
将x=4,y=0代入y=-![]() +bx+c得0=-16+4b+2,解得b=3.5
+bx+c得0=-16+4b+2,解得b=3.5
∴抛物线解析式为:y=-![]() +3.5x+2
+3.5x+2
(2)、由题意,易得M(t,-![]() t+2), N(t, -
t+2), N(t, -![]() +3.5t+2),从而MN=-
+3.5t+2),从而MN=-![]() +3.5t+2-(-
+3.5t+2-(-![]() t+2)=-
t+2)=-![]() +4t=-
+4t=-![]()
∴当t=2时,MN有最大值4
(3) 、由(2)可知,A(0,2),M(2,1),N(2,5).
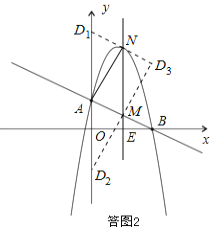
以A、M、N、D为顶点作平行四边形,D点的可能位置有三种情形,如答图2所示.
当D在y轴上时,设D的坐标为(0,a) 由AD=MN,得|a-2|=4,解得![]() =6,
=6,![]() =-2,
=-2,
从而D为(0,6)或D(0,-2)
当D不在y轴上时,由图可知D3为D1N与D2M的交点,求出直线D1N与D2M的解析式
由两解析式联立解得D为(4,4) 故所求的D点坐标为(0,6),(0,-2)或(4,4)


科目:初中数学 来源: 题型:
【题目】根据等式的性质在○里填运算符号,在□里填数
(1)x﹣18=60
x﹣18+18=60○□
x=□
(2)x+21=54
x+21﹣21=54○□
x=□
(3)![]() x=105
x=105![]()
![]() x×3=105○□
x×3=105○□
x=□
(4)4x=48
4x+4=48○□
x=□
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在七年级下册“证明”的一章的学习中,我们曾做过如下的实验:
画∠AOB=90°,并画∠AOB的平分线OC.
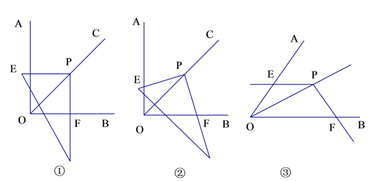
(1)把三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边分别与OA、OB相交于点E、F(如图①).度量PE、PF的长度,这两条线段相等吗?
(2)把三角尺绕点P旋转(如图②),PE与PF相等吗?请说明理由.
(3)探究:画∠AOB=50°,并画∠AOB的平分线OC,在OC上任取一点P,作∠EPF=130°.∠EPF的两边分别与OA、OB相交于E、F两点(如图③),PE与PF相等吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年茂名市生产总值约2450亿元,将2450用科学记数法表示为( )
A.0.245×104
B.2.45×103
C.24.5×102
D.2.45×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分4个等级,将调查结果绘制成如下条形统计图和扇形统计图.根据图中信息,这些学生的平均分数是( ) 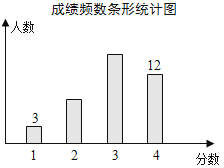

A.2.2
B.2.5
C.2.95
D.3.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列四个命题:①相等的角是对顶角;②两条直线被第三条直线所截,同位角相等;③等角的邻补角相等;④垂直于同一条直线的两条直线互相平行.其中真命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com