
【题目】在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,下面四个结论中,
①存在无数个四边形MNPQ是平行四边形;
②存在无数个四边形MNPQ是矩形;
③存在无数个四边形MNPQ是菱形;
④至少存在一个四边形MNPQ是正方形,
其中正确的结论的个数为( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据矩形的判定和性质,菱形的判定,正方形的判定,平行四边形的判定定理即可得到结论.
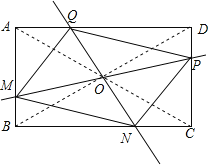
解:①如图,∵四边形ABCD是矩形,连接AC,BD交于O,
过点O直线MP和QN,分别交AB,BC,CD,AD于M,N,P,Q,
则四边形MNPQ是平行四边形,
故存在无数个四边形MNPQ是平行四边形;故正确;
②如图,当PM=QN时,四边形MNPQ是矩形,故存在无数个四边形MNPQ是矩形;故正确;
③如图,当PM⊥QN时,存在无数个四边形MNPQ是菱形;故正确;
④当四边形MNPQ是正方形时,MQ=PQ,
则△AMQ≌△DQP,
∴AM=QD,AQ=PD,
∵PD=BM,
∴AB=AD,
∴四边形ABCD是正方形,
当四边形ABCD为正方形时,四边形MNPQ是正方形,故错误;
故选:C.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
【题目】已知:点![]() 为
为![]() 边上的一个动点.
边上的一个动点.
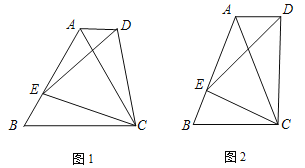
(1)如图1,若![]() 是等边三角形,以
是等边三角形,以![]() 为边在
为边在![]() 的同侧作等边
的同侧作等边![]() ,连接
,连接![]() .试比较
.试比较![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
(2)如图2,若![]() 中,
中,![]() ,以
,以![]() 为底边在
为底边在![]() 的同侧作等腰
的同侧作等腰![]() ,且
,且![]() ∽
∽![]() ,连接
,连接![]() .试判断
.试判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
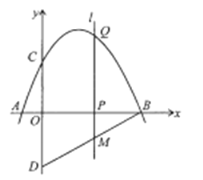
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 和点
和点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 是线段
是线段![]() 上的一个动点.设点
上的一个动点.设点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交抛物线于点
交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求抛物线的解析式;
(2)连接![]() ,
,![]() ,当点
,当点![]() 运动到何处时,
运动到何处时,![]() 面积最大?最大面积是多少?并求出此时点
面积最大?最大面积是多少?并求出此时点![]() 的坐标;
的坐标;
(3)在第![]() 问的前提下,在
问的前提下,在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 值最小,求出
值最小,求出![]() 的最小值并直接写出此时点
的最小值并直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
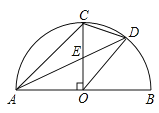
【题目】如图,AB是半圆O的直径,半径OC⊥AB于点O,点D是![]() 的中点,连接CD、OD.下列四个结论:①AC
的中点,连接CD、OD.下列四个结论:①AC![]() OD;②CE=OE;③△ODE∽△ADO;④∠ADC=∠BOD.其中正确结论的序号是( )
OD;②CE=OE;③△ODE∽△ADO;④∠ADC=∠BOD.其中正确结论的序号是( )
A.①④B.①②④C.②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
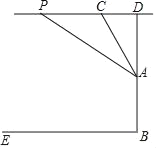
【题目】如图,滑翔运动员在空中测量某寺院标志性高塔“云端塔”的高度,空中的点P距水平地面BE的距离为200米,从点P观测塔顶A的俯角为33°,以相同高度继续向前飞行120米到达点C,在C处观测点A的俯角是60°,求这座塔AB的高度(结果精确到1米).(参考数据:sin33°≈0.54,cos33°≈0.84,tan33°≈0.65,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=﹣x+8于A,B两点,若反比例函数y=![]() (x>0)的图象与△ABC有公共点,则k的取值范围是_____.
(x>0)的图象与△ABC有公共点,则k的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
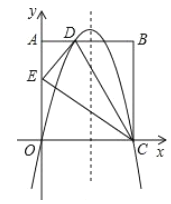
【题目】如图,在矩形![]() 中,点
中,点![]() . 沿直线
. 沿直线![]() 折叠矩形
折叠矩形![]() ,使点
,使点![]() 落在
落在![]() 边上,与点
边上,与点![]() 重合.分别以
重合.分别以![]() ,
,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 轴建立平面直角坐标系,抛物线
轴建立平面直角坐标系,抛物线![]() 经过
经过![]() 两点.
两点.
(1)求![]() 及点
及点![]() 的坐标;
的坐标;
(2)一动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒
以每秒![]() 个单位长的速度向点
个单位长的速度向点![]() 运动, 同时动点
运动, 同时动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒
以每秒![]() 个单位长的速度向点
个单位长的速度向点![]() 运动, 当点
运动, 当点![]() 运动到点
运动到点![]() 时,两点同时停止运动.设运动时间为
时,两点同时停止运动.设运动时间为![]() 秒,当
秒,当![]() 为何值时,以
为何值时,以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
(3)点![]() 在抛物线对称轴上,点
在抛物线对称轴上,点![]() 在抛物线上,是否存在这样的点
在抛物线上,是否存在这样的点![]() 与点 N,使以
与点 N,使以![]() ,
,![]() ,
,![]() ,
, ![]() 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点![]() 与点
与点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳天虹某商场从厂家批发电视机进行零售,批发价格与零售价格如下表:
电视机型号 | 甲 | 乙 |
批发价(元/台) | 1500 | 2500 |
零售价(元/台) | 2025 | 3640 |
若商场购进甲、乙两种型号的电视机共50台,用去9万元.
(1)求商场购进甲、乙型号的电视机各多少台?
(2)迎“元旦”商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种电视机销售完毕,商场共获利8.5%,求甲种型号电视机打几折销售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com