
分析 (1)本题是一道和商品的进价、标价和利润有关的实际问题,从题意中可得到相等关系有:每件商品的标价-每件商品的进价=45元;8件工艺品的利润=12件工艺品的利润.如果设进价为x元,则标价为(x+45)元,可列一元一次方程求解即可.
(2)设每件应降价a元出售,每天获得的利润为w元,根据题意可得w和a的函数关系,利用函数的性质求解即可.
解答 解:(1)设每件工艺品的进价为x元,
标价为(x+45)元,
根据题意,得:8×[85%•(x+45)-x]=12×(45-35),
解得x=155,x+45=200.
答:该工艺品每件的进价155元,标价200元.
(2)设每件应降价a元出售,每天获得的利润为w元.
则w=(45-a)(100+4a)=-4(a-10)2+4900,
当a=8时,w最大=4884元.
点评 本题考查了二次函数的性质在实际生活中的应用.最大销售利润的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在x=$-\frac{b}{2a}$时取得.


科目:初中数学 来源: 题型:解答题
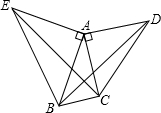 如图,△ACD、△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,∠BAC=30°,若△EAC绕某点逆时针旋转后能与△BAD重合,问:
如图,△ACD、△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,∠BAC=30°,若△EAC绕某点逆时针旋转后能与△BAD重合,问:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a(x1-x2)=d | B. | a(x2-x1)=d | C. | a(x1-x2)2=d | D. | a(x1+x2)2=d |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x6÷x2=x3 | B. | (-x)-1=$\frac{1}{x}$ | C. | (2x3)2=4x6 | D. | -2a2•a3=-2a6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
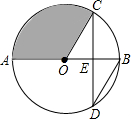 如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分的面积为( )
如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分的面积为( )| A. | π | B. | 4π | C. | $\frac{4}{3}$π | D. | $\frac{16}{3}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com