
ЁОЬтФПЁПгЩгкЮэіВЬьЦјЦЕЗЂЃЌЪаГЁЩЯЗРЛЄПкежГіЯжШШЯњЃЌФГвНвЉЙЋЫОУПдТЙЬЖЈЩњВњМзЁЂввСНжжаЭКХЕФЗРЮэіВПкежЙВ20ЭђжЛЃЌЧвЫљгаВњЦЗЕБдТШЋВПЪлГіЃЌдСЯГЩБОЁЂЯњЪлЕЅМлМАЙЄШЫЩњВњЬсГЩШчБэЃК
| Мз | вв |
дСЯГЩБО | 12 | 8 |
ЯњЪлЕЅМл | 18 | 12 |
ЩњВњЬсГЩ | 1 | 0.8 |
ЃЈ1ЃЉШєИУЙЋЫОЮхдТЗнЕФЯњЪлЪеШыЮЊ300ЭђдЊЃЌЧѓМзЁЂввСНжжаЭКХЕФВњЦЗЗжБ№ЪЧЖрЩйЭђжЛЃП
ЃЈ2ЃЉЙЋЫОЪЕааМЦМўЙЄзЪжЦЃЌМДЙЄШЫУПЩњВњвЛжЛПкежЛёЕУвЛЖЈН№ЖюЕФЬсГЩЃЌШчЙћЙЋЫОСљдТЗнЭЖШызмГЩБОЃЈдСЯзмГЩБО+ЩњВњЬсГЩзмЖюЃЉВЛГЌЙ§239ЭђдЊЃЌгІдѕбљАВХХМзЁЂввСНжжаЭКХЕФВњСПЃЌПЩЪЙИУдТЙЋЫОЫљЛёРћШѓзюДѓЃПВЂЧѓГізюДѓРћШѓЃЈРћШѓ=ЯњЪлЪеШыЉЭЖШызмГЩБОЃЉ
ЁОД№АИЁПЃЈ1ЃЉМзЁЂввСНжжаЭКХЕФВњЦЗЗжБ№ЮЊ10ЭђжЛЃЌ10ЭђжЛЃЛЃЈ2ЃЉЕБy=15ЪБЃЌWзюДѓЃЌзюДѓжЕЮЊ91ЭђдЊЃЎ
ЁОНтЮіЁП
ЕквЛЮЪЩшЮДжЊЪ§ЃЌНЈСЂЕШСПЙиЯЕЃЌНтвЛдЊвЛДЮЗНГЬЃЛЕкЖўЮЪЃЌЯШИљОнЬтФПжаЕФЬѕМўШЗЖЈБфСПЕФЗЖЮЇЃЌШЛКѓдйСаГіРћШѓЕФБэДяЪНЃЌЧѓРћШѓКЏЪ§дкИУЗЖЮЇЩЯЕФзюДѓжЕМДЮЊзюДѓРћШѓ.
ЃЈ1ЃЉЩшМзаЭКХЕФВњЦЗгаxЭђжЛЃЌдђвваЭКХЕФВњЦЗгаЃЈ20ЉxЃЉЭђжЛЃЌ
ИљОнЬтвтЕУЃК18x+12ЃЈ20ЉxЃЉ=300ЃЌ
НтЕУЃКx=10ЃЌ
дђ20Љx=20Љ10=10ЃЌ
дђМзЁЂввСНжжаЭКХЕФВњЦЗЗжБ№ЮЊ10ЭђжЛЃЌ10ЭђжЛЃЛ
ЃЈ2ЃЉЩшАВХХМзаЭКХВњЦЗЩњВњyЭђжЛЃЌдђвваЭКХВњЦЗЩњВњЃЈ20ЉyЃЉЭђжЛЃЌ
ИљОнЬтвтЕУЃК13y+8.8ЃЈ20ЉyЃЉЁм239ЃЌ
НтЕУЃКyЁм15ЃЌ
ИљОнЬтвтЕУЃКРћШѓW=ЃЈ18Љ12Љ1ЃЉy+ЃЈ12Љ8Љ0.8ЃЉЃЈ20ЉyЃЉ=1.8y+64ЃЌ
ЕБy=15ЪБЃЌWзюДѓЃЌзюДѓжЕЮЊ91ЭђдЊЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌе§ЗНаЮA1B1C1D1ЁЂD1 E1E2B2ЁЂA2B2 C2D2ЁЂD2 E3E4B3ЁЁАДШчЭМЫљЪОЕФЗНЪНЗХжУЃЌЦфжаЕуB1дкyжсЩЯЃЌЕуC1ЁЂE1ЁЂE2ЁЂC2ЁЂE3ЁЂE4ЁЂC3ЁЁдкxжсЩЯЃЌвбжЊе§ЗНаЮA1B1C1D1ЕФБпГЄЮЊlЃЌЁЯB1C1O= 60Ёу, B1C1ЁЮB2C2ЁЮB3C3ЁЁЃЌдђе§ЗНаЮA2017B2017 C2017 D2017ЕФБпГЄЪЧЃЈ ЃЉ

A. ЃЈ![]() ЃЉ2016 B. ЃЈ
ЃЉ2016 B. ЃЈ![]() ЃЉ2017 C. ЃЈ
ЃЉ2017 C. ЃЈ![]() ЃЉ2016 D. ЃЈ
ЃЉ2016 D. ЃЈ![]() ЃЉ2017
ЃЉ2017
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпy=ax2+bx+3ЃЈaЁй0ЃЉОЙ§ЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ![]() ЃЌ0ЃЉЃЌЧвгыyжсЯрНЛгкЕуCЃЎ
ЃЌ0ЃЉЃЌЧвгыyжсЯрНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓетЬѕХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉЧѓЁЯACBЕФЖШЪ§ЃЛ
ЃЈ3ЃЉЕуDЪЧХзЮяЯпЩЯЕФвЛЖЏЕуЃЌЪЧЗёДцдкЕуDЃЌЪЙЕУtanЁЯDCB=tanЁЯACOЃЎШєДцдкЃЌЧыЧѓГіЕуDЕФзјБъЃЌШєВЛДцдкЃЌЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНааЫФБпаЮABCDжаЃЌЕуAдкЗДБШР§КЏЪ§y=![]() ЃЈkЁй0ЃЉЕФЭМЯѓЩЯЃЌЕуDдкyжсЩЯЃЌЕуBЁЂЕуCдкxжсЩЯЃЎШєЦНааЫФБпаЮABCDЕФУцЛ§ЮЊ10ЃЌдђkЕФжЕЪЧЃЈЁЁЁЁЃЉ
ЃЈkЁй0ЃЉЕФЭМЯѓЩЯЃЌЕуDдкyжсЩЯЃЌЕуBЁЂЕуCдкxжсЩЯЃЎШєЦНааЫФБпаЮABCDЕФУцЛ§ЮЊ10ЃЌдђkЕФжЕЪЧЃЈЁЁЁЁЃЉ

A. Љ10 B. Љ5 C. 5 D. 10
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИпПеЕФЦјЮТгыОрЕиУцЕФИпЖШгаЙиЃЌФГЕиОрЕиУцЕФИпЖШУПЩ§Ип1kmЃЌЦјЮТЯТНЕ6ЁцЃЌвбжЊЕиУцЦјЮТЮЊ20Ёц.
(1)аДГіИУЕиПежаЦјЮТT(Ёц)гыИпЖШh(km)жЎМфЕФКЏЪ§БэДяЪН.
(2)ЧѓОрРыЕиУцЩЯ4kmДІЕФЦјЮТT.
(3)ЧѓЦјЮТЮЊ-16ЁцДІОрЕиУцЕФИпЖШh.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌжБЯпlЃКy=![]() x+mгыxжсЁЂyжсЗжБ№НЛгкЕуAКЭЕуBЃЈ0ЃЌЉ1ЃЉЃЌХзЮяЯпy=
x+mгыxжсЁЂyжсЗжБ№НЛгкЕуAКЭЕуBЃЈ0ЃЌЉ1ЃЉЃЌХзЮяЯпy=![]() x2+bx+cОЙ§ЕуBЃЌгыжБЯпlЕФСэвЛИіНЛЕуЮЊCЃЈ4ЃЌnЃЉЃЎ
x2+bx+cОЙ§ЕуBЃЌгыжБЯпlЕФСэвЛИіНЛЕуЮЊCЃЈ4ЃЌnЃЉЃЎ
ЃЈ1ЃЉЧѓnЕФжЕКЭХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуDдкХзЮяЯпЩЯЃЌDEЁЮyжсНЛжБЯпlгкЕуEЃЌЕуFдкжБЯпlЩЯЃЌЧвЫФБпаЮDFEGЮЊОиаЮЃЈШчЭМ2ЃЉЃЌЩшЕуDЕФКсзјБъЮЊtЃЈ0ЃМtЃМ4ЃЉЃЌОиаЮDFEGЕФжмГЄЮЊpЃЌЧѓpгыtЕФКЏЪ§ЙиЯЕЪНвдМАpЕФзюДѓжЕЃЛ
ЃЈ3ЃЉНЋЁїAOBШЦЦНУцФкФГЕуMа§зЊ90ЁуЛђ180ЁуЃЌЕУЕНЁїA1O1B1ЃЌЕуAЁЂOЁЂBЕФЖдгІЕуЗжБ№ЪЧЕуA1ЁЂO1ЁЂB1ЃЎШєЁїA1O1B1ЕФСНИіЖЅЕуЧЁКУТфдкХзЮяЯпЩЯЃЌФЧУДЮвУЧОЭГЦетбљЕФЕуЮЊЁАТфЕуЁБЃЌЧыжБНгаДГіЁАТфЕуЁБЕФИіЪ§КЭа§зЊ180ЁуЪБЕуA1ЕФКсзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
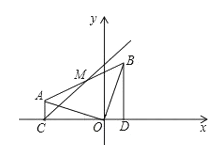
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжагавЛЁїBODЃЌ![]() ЃЌАб BO ШЦЕуO ФцЪБеыа§зЊ 90ЁуЕУOAЃЌ СЌНгABЃЌзї
ЃЌАб BO ШЦЕуO ФцЪБеыа§зЊ 90ЁуЕУOAЃЌ СЌНгABЃЌзї![]() гкЕу CЃЌЕуB ЕФзјБъЮЊЃЈ1ЃЌ3ЃЉ.
гкЕу CЃЌЕуB ЕФзјБъЮЊЃЈ1ЃЌ3ЃЉ.
ЃЈ1ЃЉЧѓжБЯпAB ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєAB жаЕуЮЊ MЃЌСЌНг CMЃЌЖЏЕу PЁЂQ ЭЌЪБДг C ЕуГіЗЂЃЌЕу P биЩфЯпCM вдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЕуQбиЯпЖЮCD вдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕу D дЫЖЏЃЌЕБQЕудЫЖЏЕНD ЕуЪБЃЌPЁЂQЭЌЪБЭЃжЙдЫЖЏЃЌЩшЁїPQO ЕФУцЛ§ЮЊ SЃЈ![]() ЃЉЃЌдЫЖЏЪБМфЮЊtУыЃЌЧѓSгыtЕФКЏЪ§ЙиЯЕЪНЃЌВЂжБНгаДГіздБфСПtЕФШЁжЕЗЖЮЇЃЛ
ЃЉЃЌдЫЖЏЪБМфЮЊtУыЃЌЧѓSгыtЕФКЏЪ§ЙиЯЕЪНЃЌВЂжБНгаДГіздБфСПtЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЪЧЗёДцдкетбљЕФ P ЕуЃЌЪЙЕУPЁЂOЁЂBЮЊЖЅЕуЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЖдгІЕФt жЕКЭДЫЪБQЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦНУцжБНЧзјБъЯЕxOyжаЃЌЙ§дЕуOМАЕуAЃЈ0ЃЌ4ЃЉЁЂCЃЈ12ЃЌ0ЃЉзїОиаЮOABCЃЌЁЯAOCЕФЦНЗжЯпНЛABгкЕуDЃЎЕуPДгЕуOГіЗЂЃЌвдУПУы2![]() ИіЕЅЮЛГЄЖШЕФЫйЖШбиЩфЯпODЗНЯђвЦЖЏЃЛЭЌЪБЕуQДгЕуOГіЗЂЃЌвдУПУы4ИіЕЅЮЛГЄЖШЕФЫйЖШбиxжсе§ЗНЯђвЦЖЏЃЎЩшвЦЖЏЪБМфЮЊtУыЃЎ
ИіЕЅЮЛГЄЖШЕФЫйЖШбиЩфЯпODЗНЯђвЦЖЏЃЛЭЌЪБЕуQДгЕуOГіЗЂЃЌвдУПУы4ИіЕЅЮЛГЄЖШЕФЫйЖШбиxжсе§ЗНЯђвЦЖЏЃЎЩшвЦЖЏЪБМфЮЊtУыЃЎ

ЃЈ1ЃЉЕБЕуPвЦЖЏЕНЕуDЪБЃЌЧѓГіДЫЪБtЕФжЕЃЎ
ЃЈ2ЃЉЕБtЮЊКЮжЕЪБЃЌЁїPQBЮЊжБНЧШ§НЧаЮЃЎ
ЃЈ3ЃЉвбжЊЙ§OЁЂPЁЂQШ§ЕуЕФХзЮяЯпНтЮіЪНЮЊy=Љ![]() ЃЎЮЪЪЧЗёДцдкФГвЛЪБПЬtЃЌНЋЁїPQBШЦФГЕуа§зЊ180ЁуКѓЃЌШ§ИіЖдгІЖЅЕуЧЁКУЖМТфдкЩЯЪіХзЮяЯпЩЯЃПШєДцдкЃЌЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЎЮЪЪЧЗёДцдкФГвЛЪБПЬtЃЌНЋЁїPQBШЦФГЕуа§зЊ180ЁуКѓЃЌШ§ИіЖдгІЖЅЕуЧЁКУЖМТфдкЩЯЪіХзЮяЯпЩЯЃПШєДцдкЃЌЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЬНЫїЙцТЩЃКЯТСаЭМАИЪЧЩНЮїНњЩЬДѓдКДАИёЕФвЛВПЗжЃЌЦфжаЁАЁ№ЁБДњБэДАжНЩЯЫљЬљЕФМєжНЃЌЫцзХЛљБОЭМАИЕФдіМгЫљЬљМєжНЁАЁ№ЁБЕФзмИіЪ§вВдкЗЂЩњБфЛЏ.

ЃЈ1ЃЉЬюаДЯТБэЃК
Ек | 1 | 2 | 3 | 4 | ЁЁ |
ЁАЁ№ЁБЕФзмИіЪ§ | ЁЁ |
ЃЈ2ЃЉЧыФуаДГіЕк![]() ИіЭМАИжаЁАЁ№ЁБЕФзмИіЪ§
ИіЭМАИжаЁАЁ№ЁБЕФзмИіЪ§![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪН.
жЎМфЕФКЏЪ§ЙиЯЕЪН.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com