练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，将长方形ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F，已知∠BDC=62°，则∠DFE的度数为（ ）

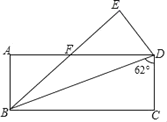
    A. 62°B. 56°C. 31°D. 28°

    【答案】B

    【解析】

    先利用互余计算出∠FDB=28°，再根据平行线的性质得∠CBD=∠FDB=28°，接着根据折叠的性质得∠FBD=∠CBD=28°，然后利用三角形外角性质计算∠DFE的度数

    ∵四边形ABCD为矩形，

    ∴AD∥BC,∠ADC=90°，

    ∵∠FDB=90°∠BDC=90°62°=28°，

    ∵AD∥BC，

    ∴∠CBD=∠FDB=28°，

    ∵矩形ABCD沿对角线BD折叠，

    ∴∠FBD=∠CBD=28°，

    ∴∠DFE=∠FBD+∠FDB=28°+28°=56°.

    故选：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

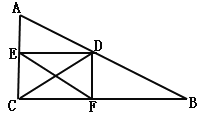
    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=2，BC=4，点D为边AB上一动点，DE⊥AC，DF⊥BC，垂足为E，F. 连接EF，CD.

    （1）求证：EF＝CD；

    （2）当EF为何值时，EF∥AB；

    （3）当四边形ECFD为正方形时，求EF的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

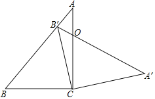
    【题目】如图，△ABC中，∠ACB＝90°,∠B＝50°,△ABC绕点C顺时针旋转得到△A′B′C，点B′恰好落在线段AB上，AC、A′B′相交于O，则∠COA′的度数为_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=x2+bx+c经过△ABC的三个顶点，其中点A（0，1），点B（﹣9，10），AC∥x轴，点P时直线AC下方抛物线上的动点．

    （1）求抛物线的解析式；（2）过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标；

    （3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是按照一定规律画出的“树形图”，经观察可以发现：图A2比图A1多出2个“树枝”，图A3比图A2多出4个“树枝”，图A4比图A3多出8个“树枝”……照此规律，图A6比图A2多出“树枝”( )

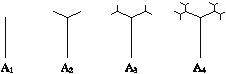
    A.32个B.56个C.60个D.64个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数y=ax2+bx+c的图象与x轴的交点A，B的横坐标分别为﹣1，3．与y轴负半轴交于点C，在下面四个结论中：①ac＜0；②2a﹣b=0；③a+b+c＞0；④c=﹣3a．其中正确的结论有（　　）

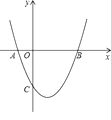
    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD和正方形CEFG的面积分别为4 cm2,36cm2, 点G,C,B在一条直线上，M是BF的中点，则点M到GD的距离为_________cm．

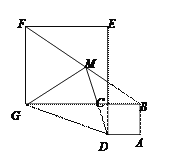
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“1285个服务站点”，“4.1万辆公共自行车”，“日均租骑量32.54万次”，“1小时内免费”，…，自2012年开通运营以来，太原公共自行车已经伴随太原市民走过近七个春秋.课外活动小组的同学们，在某双休日11:30-12:00对我市某个公共自行车服务站点的租骑量进行了观察记录.用“-6”表示骑走了6辆自行车，记录结果如下表(时间段不含前一时刻但含后一时刻，如11:30-11:35不含11:30但含11:35)

    时间段

    11:30-11:35

    11:35-11:40

    11:40-11:45

    11:45-11:50

    11:50-11:55

    11:55-12:00

    自行车数量

    -15

    +8

    -11

    +10

    -6

    +13

    假设此服务站点在11:30时有自行车30辆，则在12:00时该站点有自行车( )

    A.31辆B.30辆C.29辆D.27辆

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：a、b、c满足a=-b,|a+1|+（c-4）2=0，请回答问题:

    （1）请求出a、b、c的值；

    （2）a、b、c所对应的点分别为A、B、C，P为数轴上一动点，其对应的数为x，若点P在线段BC上时，请化简式子：|x+1|-|1-x|+2|x-4|（请写出化简过程）；

    （3）若点P从A点出发，以每秒2个单位长度的速度向右运动，试探究当点P运动多少秒时，PC=3PB?

    查看答案和解析>>

    同步练习册答案