
【题目】已知:a、b、c满足a=-b,|a+1|+(c-4)2=0,请回答问题:
(1)请求出a、b、c的值;
(2)a、b、c所对应的点分别为A、B、C,P为数轴上一动点,其对应的数为x,若点P在线段BC上时,请化简式子:|x+1|-|1-x|+2|x-4|(请写出化简过程);
![]()
(3)若点P从A点出发,以每秒2个单位长度的速度向右运动,试探究当点P运动多少秒时,PC=3PB?
【答案】(1)a=-1, b=1,c=4;(2)-2x+10;(3)![]() 或
或![]() 秒
秒
【解析】试题分析:
(1) 利用“若几个非负数之和为零则每一个非负数均为零”这一结论,可以得到a与c的值. 利用已知条件容易得到b的值.
(2) 根据“点P在线段BC上”可以得到x的取值范围. 根据x的取值范围,可以依次确定待化简式子中绝对值符号内的整式值的符号,再根据绝对值的代数意义去掉相应的绝对值符号,然后合并同类项即可得出答案.
(3) 设点P的运动时间为t秒. 分析题意可知,要想得到符合题意的运动时间,就需要获得线段PC与线段PB的长关于运动时间t的表达式. 对于线段PC的表达式,可以通过PC=AC-AP的关系得到. 线段AC的长易知;由于点P从点A出发沿直线向右运动,所以线段AP的长代表了点P的运动路程. 根据“路程等于速度乘以时间”这一等量关系,可以用t表示出线段AP的长. 对于线段PB的表达式,则需要按照点P与点B的相对位置进行讨论. 当点P在点B的左侧时,可根据PB=AB-AP获得线段PB的表达式;当点P在点B的右侧时,可根据PB=AP-AB获得线段PB的表达式. 在获得上述表达式后,利用等量关系PC=3PB列出方程求解时间t即可.
试题解析:
(1) 因为![]() ,所以a+1=0,c-4=0,即a=-1,c=4.
,所以a+1=0,c-4=0,即a=-1,c=4.
因为a=-b,a=-1,所以b=-a=-(-1)=1.
综上所述,a=-1,b=1,c=4.
(2) 因为点P在线段BC上,b=1,c=4,所以![]() .
.
因为![]() ,所以x+1>0,
,所以x+1>0, ![]() ,
, ![]() .
.
当x+1>0时, ![]() ;
;
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() .
.
因此,当点P在线段BC上(即![]() )时,
)时,
![]()
=![]()
= ![]()
=![]() .
.
(3) 设点P的运动时间为t秒.
因为点P从A点出发,以每秒2个单位长度的速度向右运动,所以AP=2t.
因为点A对应的数为-1,点C对应的数为4,所以AC=4-(-1)=5.
因为PC=3PB,所以PC>PB. 故点P不可能在点C的右侧.
因此,PC=AC-AP.
因为AP=2t,AC=5,所以PC=AC-AP=5-2t.
分析本小题的题意,点P与点B的位置关系没有明确的限制,
故本小题应该对以下两种情况分别进行求解.
①点P在点B的左侧,如下图.
![]()
因为点A对应的数为-1,点B对应的数为1,所以AB=1-(-1)=2.
因为AP=2t,AB=2,所以PB=AB-AP=2-2t.
因为PC=3PB,PC=5-2t,PB=2-2t,所以5-2t=3(2-2t).
解这个关于t的一元一次方程,得 ![]() .
.
②点P在点B的右侧,如下图.
![]()
因为AP=2t,AB=2,所以PB=AP-AB=2t-2.
因为PC=3PB,PC=5-2t,PB=2t-2,所以5-2t=3(2t-2).
解这个关于t的一元一次方程,得 ![]() .
.
综上所述,当点P运动![]() 或
或![]() 秒时,PC=3PB.
秒时,PC=3PB.


科目:初中数学 来源: 题型:
【题目】如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.其中正确的个数是

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,直线l1经过(2,3)和(-1,-3):直线l2经过原点O,且与直线l1交于点P(-2,a).
(1)求a的值;
(2)(-2,a)可看成怎样的二元一次方程组的解?
查看答案和解析>>
科目:初中数学 来源: 题型:
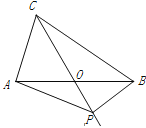
【题目】如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 __________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校一栋5层的教学大楼,第一层没有教室,二至五层,每层楼有6间教室,进出这栋大楼共有两道大小相同的大门和一道小门(平时小门不开).安全检查中,对这3道门进行了测试:当同时开启一道大门和一道小门时,3分钟内可以通过540名学生,若一道大门平均每分钟比一道小门可多通过60名学生.
(1)求平均每分钟一道大门和一道小门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率降低20%.安全检查规定:在紧急情况下全大楼的学生应在5分钟内安全撤离.这栋教学大楼每间教室平均有45名学生,问:在紧急情况下只开启两道大门是否可行?为什么?3道门都开启呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,DEF分别为△ABC边ACABBC上的点,∠A=∠1=∠C,DE=DF.下面的结论一定成立的是( )
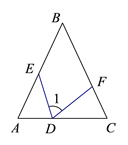
A. AE=FC B. AE=DE C. AE+FC=AC D. AD+FC=AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a,b互为相反数,b,c互为倒数,且m的立方等于它本身.
(Ⅰ)求ac的值;
(Ⅱ)若a>1,且m<0,![]() ,求6(2a﹣S)+(S﹣2a)的值;
,求6(2a﹣S)+(S﹣2a)的值;
(III)若m≠0,试讨论:当x为有理数时,|x+m|﹣|x﹣m|是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:
(1)(-14)-(-15) (2) 23×(1-![]() )×0.5.
)×0.5.
(3)![]() ×(-5)(用简便方法计算) (4) (1-
×(-5)(用简便方法计算) (4) (1-![]() +
+![]() )×(-48)
)×(-48)
(5)(-10)÷![]() ×2 +(-4)3; (6)-12-(
×2 +(-4)3; (6)-12-(![]() -
-![]() )÷
)÷![]() ×[-2+(-3)2].
×[-2+(-3)2].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com