
【题目】计算题:
(1)(-14)-(-15) (2) 23×(1-![]() )×0.5.
)×0.5.
(3)![]() ×(-5)(用简便方法计算) (4) (1-
×(-5)(用简便方法计算) (4) (1-![]() +
+![]() )×(-48)
)×(-48)
(5)(-10)÷![]() ×2 +(-4)3; (6)-12-(
×2 +(-4)3; (6)-12-(![]() -
-![]() )÷
)÷![]() ×[-2+(-3)2].
×[-2+(-3)2].
【答案】(1)1;(2)3;(3)-2497;(4)-76;;(5)-104;(6)![]()
【解析】
(1)根据减法法则计算即可;
(2)先算乘方和括号,再算乘法即可;
(3)把![]() 拆为500-
拆为500-![]() ,再根据乘法的分配律计算即可;
,再根据乘法的分配律计算即可;
(4)根据乘法的分配律计算即可;
(5)先算乘方,再算乘除,后算加减即可;
(6)先算乘方和括号,再算乘除,后算加减即可.
(1)原式=(-14)+(+15)=1;
(2)原式= 8×![]() ×
×![]() =3;
=3;
(3)原式=(500-![]() )×(-5)
)×(-5)
=500×(-5)-![]() ×(-5)
×(-5)
=-2500+3
=-2497;
(4)原式=1×(-48)-![]() ×(-48)+
×(-48)+![]() ×(-48)
×(-48)
=-48+8-36
=-76;
(5)原式=(-10)×2×2 +(-64)
=(-40)+(-64)
=-104;
(6)原式=-1-(-![]() )×3×[-2+9]
)×3×[-2+9]
=-1-(-![]() )×3×7
)×3×7
=-1+![]()
=![]() .
.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】已知:a、b、c满足a=-b,|a+1|+(c-4)2=0,请回答问题:
(1)请求出a、b、c的值;
(2)a、b、c所对应的点分别为A、B、C,P为数轴上一动点,其对应的数为x,若点P在线段BC上时,请化简式子:|x+1|-|1-x|+2|x-4|(请写出化简过程);
![]()
(3)若点P从A点出发,以每秒2个单位长度的速度向右运动,试探究当点P运动多少秒时,PC=3PB?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=﹣x+4于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.

(1)求抛物线的表达式;
(2)点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中△AOC与△OBD重叠部分的面积记为S,试求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例如图,线段AB=1=0﹣(﹣1);线段 BC=2=2﹣0;线段 AC=3=2﹣(﹣1)问题
①数轴上点M、N代表的数分别为﹣9和1,则线段MN= ;
②数轴上点E、F代表的数分别为﹣6和﹣3,则线段EF= ;
③数轴上的两个点之间的距离为5,其中一个点表示的数为2,则另一个点表示的数为m,求m.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() =
=![]() (
(![]() ≠0)与
≠0)与![]() 轴交于AB两点,与
轴交于AB两点,与![]() 轴交于C点,其对称轴为
轴交于C点,其对称轴为![]() =1,且A(-1,0)C(0,2).
=1,且A(-1,0)C(0,2).
(1)直接写出该抛物线的解析式;
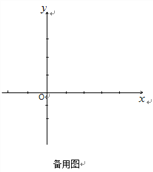
(2)P是对称轴上一点,△PAC的周长存在最大值还是最小值?请求出取得最值(最大值或最小值)时点P的坐标;
(3)设对称轴与![]() 轴交于点H,点D为线段CH上的一动点(不与点CH重合).点P是(2)中所求的点.过点D作DE∥PC交
轴交于点H,点D为线段CH上的一动点(不与点CH重合).点P是(2)中所求的点.过点D作DE∥PC交![]() 轴于点E.连接PDPE.若CD的长为
轴于点E.连接PDPE.若CD的长为![]() ,△PDE的面积为S,求S与
,△PDE的面积为S,求S与![]() 之间的函数关系式,试说明S是否存在最值,若存在,请求出最值,并写出S取得的最值及此时
之间的函数关系式,试说明S是否存在最值,若存在,请求出最值,并写出S取得的最值及此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真阅读材料,并解决下面问题:
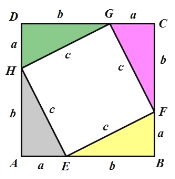
(1)以 a 、b 为直角边,以 c 为斜边做四个全等的直角三角形,把这四个直角三角形拼成如图所示形状,使 A 、 E 、 B 三点在一条直线上, B 、 F 、C 三点在一条直线上, C 、G 、D 三点在一条直线上。容易得到:四边形 ABCD 和四边形 EFGH 均是正方形;请用两个不同的代数式 和 表示正方形ABCD 的面积;于是可得到直角三角形关于三边的一个重要的等量关系是 (用含字母 a 、b 、 c 的最简式子填空)
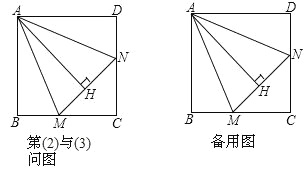
(2)如图,已知正方形 ABCD 中,MAN 45 ,MAN 绕点A 顺时针旋转,它的两边分别交CB 、DC 于点 M 、 N , AH MN 于点 H 。请问: MN 与BM 、 DN 之间有何数量关系?请说明理由;
(3)如图,在(2)的情况下,
①请判断 AH 与 AB 之间的数量关系,并说明理由;
②已知 AH 12 ,若 N 还是CD 的中点,结合(1)的结论,求 BM 的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
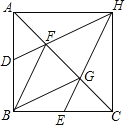
【题目】已知:如图,在△ABC中,AB=BC,∠ABC=90°,点D、E分别是边AB、BC的中点,点F、G是边AC的三等分点,DF、EG的延长线相交于点H,连接HA、HC.
(1)求证:四边形FBGH是菱形;
(2)求证:四边形ABCH是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下,对于数![]() 和
和![]() ,
,![]() (≠,不等号),但是对于某些特殊的数
(≠,不等号),但是对于某些特殊的数![]() 和
和![]() ,
,![]() 我们把这些特殊的数
我们把这些特殊的数![]() 和
和![]() ,称为“理想数对”,记作
,称为“理想数对”,记作![]() .例如当
.例如当![]() 时,有
时,有![]() ,那么
,那么![]() 就是“理想数对”.
就是“理想数对”.
(1)![]() 可以称为“理想数对”的是 ;
可以称为“理想数对”的是 ;
(2)如果![]() 是“理想数对”,那么
是“理想数对”,那么![]() = ;
= ;
(3)若![]() 是“理想数对”,求
是“理想数对”,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com