Question

【题目】请认真阅读材料，并解决下面问题：

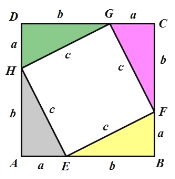
（1）以 a 、b 为直角边，以 c 为斜边做四个全等的直角三角形，把这四个直角三角形拼成如图所示形状，使 A 、 E 、 B 三点在一条直线上， B 、 F 、C 三点在一条直线上， C 、G 、D 三点在一条直线上。容易得到：四边形 ABCD 和四边形 EFGH 均是正方形；请用两个不同的代数式 和 表示正方形ABCD 的面积；于是可得到直角三角形关于三边的一个重要的等量关系是 （用含字母 a 、b 、 c 的最简式子填空）

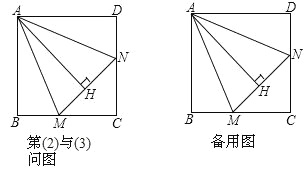
（2）如图，已知正方形 ABCD 中，MAN 45 ，MAN 绕点A 顺时针旋转，它的两边分别交CB 、DC 于点 M 、 N ， AH MN 于点 H 。请问： MN 与BM 、 DN 之间有何数量关系？请说明理由；

（3）如图，在（2）的情况下，

①请判断 AH 与 AB 之间的数量关系，并说明理由；

②已知 AH 12 ，若 N 还是CD 的中点，结合（1）的结论，求 BM 的长。

Answer 1

【答案】(1) （a+b）2，2ab+c2，c2=a2+b2; (2)见详解；（3）①AB=AH；②4.

【解析】

（1）根据正方形ABCD的面积等于边长的平方或者等于4个全等的直角三角形与正方形EFGH的面积和，可列出不同的代数式，根据代数式可得等量关系式；
（2）延长CB，使BE=DN，连接AE，由题意可证△ABE≌△ADN，可得AE=AN，∠EAB=∠DAN，可得∠EAM=∠MAN=45°，即可证△EAM≌△NAM，
即可得MN=DN+BM；
（3）①由△EAM≌△NAM，可得S△EAM=S△NAM，即×EM×AB=×MN×AH，且EM=MN，可得AB=AH；
②由题意可求BC=AB=CD=12，CN=DN=BE=6，根据勾股定理可求BM的长．

解：（1）∵正方形ABCD的面积=（a+b）2，正方形ABCD的面积=4×ab+c2=c2+2ab
∴c2=a2+b2
故答案为：（a+b）2，2ab+c2，c2=a2+b2．
（2）MN=BM+DN
如图：延长CB，使BE=DN，连接AE

∵四边形ABCD是正方形
∴AB=AD=BC=CD，∠ADC=∠ABC=∠BCD=90°=∠BAD
∵BE=DN，AB=AD，∠ADC=∠ABE
∴△ABE≌△ADN（SAS）
∴AE=AN，∠EAB=∠DAN
∵∠MAN=45°，∠BAD=90°
∴∠BAM+∠DAN=45°
∴∠BAM+∠EAB=45°
∴∠EAM=∠MAN，且AM=AM，AE=AN
∴△EAM≌△NAM（SAS）
∴MN=EM
∵EM=BM+BE=BM+DN
∴MN=BM+DN
（3）①∵△EAM≌△NAM
∴S△EAM=S△NAM
∴×EM×AB=×MN×AH，且EM=MN
∴AB=AH
②∵AH=12，
∴AB=12
∴CD=BC=12
∵点N是CD的中点
∴CN=DN=BE=6
∴MN=BM+6
在Rt△MNC中，MN2=CM2+CN2．
∴（BM+6）2=（12-BM）2+36
∴BM=4