
【题目】如图,∠AOB是平角,OD是∠AOC的角平分线,∠COE=∠BOE.

(1)若∠AOC= 50°,则∠DOE= °;
(2)当∠AOC的大小发生改变时,∠DOE的大小是否发生改变?为什么?
(3)图中与∠COD互补角的个数随∠AOC的度数变化而变化,直接写出与∠COD互补的角的个数及对应的∠AOC的度数.
【答案】(1)90°;(2)不发生改变,∠DOE=90°,理由见解析;(3)∠AOC=90°时,存在与∠COD互补的角有三个分别为∠BOD、∠BOE,∠COE,.∠AOC=120°时,存在与∠COD互补的角有两个分别为∠BOD、∠AOC.∠AOC其它角度时,存在与∠COD互补的角有一个为∠BOD.
【解析】
(1)根据补角的定义,可以推断出∠BOC的度数,由∠COE=∠BOE,可以求出∠COE和∠BOE的度数,根据角平分线的性质和∠AOC的度数,可以求出∠COD的度数,从而求出∠DOE的度数,可以推断出∠AOC=∠AOE,在根据角平分线的性质,可以得到∠AOD=∠COD,得出∠AOD的度数,即可解决.
(2)设∠AOC的度数为2x,用含x的式子表示出∠DOE,看是否是一个定值,然后判断即可.
(3)因为OD是∠AOC的角平分线,所以![]() ,求与∠COD互补的角,即求与∠AOD互补的角,根据题目中的角的关系判断写出即可.
,求与∠COD互补的角,即求与∠AOD互补的角,根据题目中的角的关系判断写出即可.
(1)![]()
![]()
![]()
![]()
![]()
又∵OD是∠AOC的角平分线
![]()
![]() ;
;
(2)不发生改变,设∠AOC=2x.
∵OD是∠AOC的平分线
∴∠AOD=∠COD=x
∠BOC=180° 2x
∵∠COE=∠BOE
∴∠COE=![]() =90°+x
=90°+x
∴∠DOE=90°+x x=90°
(3)∠AOC=90°时,存在与∠COD互补的角有三个分别为∠BOD、∠BOE,∠COE,如图
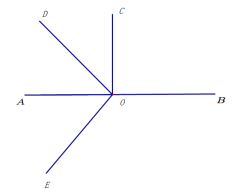
∠AOC=120°时,存在与∠COD互补的角有两个分别为∠BOD、∠AOC.如图

∠AOC其它角度时,存在与∠COD互补的角有一个为∠BOD.如图:


科目:初中数学 来源: 题型:
【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题:
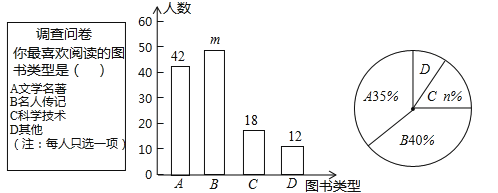
(1)本次调查共抽查了 名学生;
(2)两幅统计图中的m= ,n= .
(3)已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建设银行的某储蓄员小张在办理业务时,约定存入为正,取出为负. 2019年10月29日,他先后办理了七笔业务: +2000元、-800元、+400元、-800元、+1400元、-1700元、-200元.
(1)若他早上领取备用金4000元,那么下班时应交回银行_________元钱.
(2)请判断在这七次办理业务中,小张在第_______次业务办理后手中现金最多,第_________次业务办理后手中现金最少.
(3)若每办一件业务,银行发给业务量的0.2%作为奖励,小张这天应得奖金多少元?
(4)若记小张第一次办理业务前的现金为0点,用折线统计图表示这7次业务办理中小张手中现金的变化情况.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例如图,线段AB=1=0﹣(﹣1);线段 BC=2=2﹣0;线段 AC=3=2﹣(﹣1)问题
①数轴上点M、N代表的数分别为﹣9和1,则线段MN= ;
②数轴上点E、F代表的数分别为﹣6和﹣3,则线段EF= ;
③数轴上的两个点之间的距离为5,其中一个点表示的数为2,则另一个点表示的数为m,求m.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
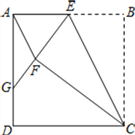
【题目】如图,正方形ABCD中,点E为AB上一动点(不与A、B重合).将△EBC沿CE翻折至△EFC,延长EF交边AD于点G.
(1)连结AF,若 AF∥CE.证明:点E为AB的中点;
(2)证明:GF=GD;
(3)若AD=10,设EB=x,GD=y,求y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真阅读材料,并解决下面问题:
(1)以 a 、b 为直角边,以 c 为斜边做四个全等的直角三角形,把这四个直角三角形拼成如图所示形状,使 A 、 E 、 B 三点在一条直线上, B 、 F 、C 三点在一条直线上, C 、G 、D 三点在一条直线上。容易得到:四边形 ABCD 和四边形 EFGH 均是正方形;请用两个不同的代数式 和 表示正方形ABCD 的面积;于是可得到直角三角形关于三边的一个重要的等量关系是 (用含字母 a 、b 、 c 的最简式子填空)
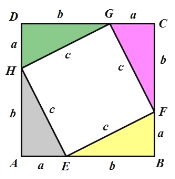
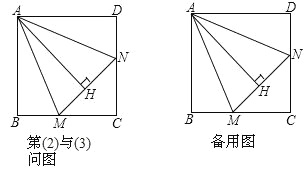
(2)如图,已知正方形 ABCD 中,MAN 45 ,MAN 绕点A 顺时针旋转,它的两边分别交CB 、DC 于点 M 、 N , AH MN 于点 H 。请问: MN 与BM 、 DN 之间有何数量关系?请说明理由;
(3)如图,在(2)的情况下,
①请判断 AH 与 AB 之间的数量关系,并说明理由;
②已知 AH 12 ,若 N 还是CD 的中点,结合(1)的结论,求 BM 的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列各数填在相应的集合里.
﹣![]() ,9,0,+4.3,|﹣0.5|,﹣(+7),18%,(﹣3)4,﹣(﹣2)5,﹣62
,9,0,+4.3,|﹣0.5|,﹣(+7),18%,(﹣3)4,﹣(﹣2)5,﹣62
正有理数集合:{…};
正分数集合:{…};
负整数集合:{…};
自然数集合:{…}.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com