
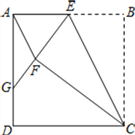
【题目】如图,正方形ABCD中,点E为AB上一动点(不与A、B重合).将△EBC沿CE翻折至△EFC,延长EF交边AD于点G.
(1)连结AF,若 AF∥CE.证明:点E为AB的中点;
(2)证明:GF=GD;
(3)若AD=10,设EB=x,GD=y,求y与x的函数关系式.
【答案】(1)证明见解析;(2)证明见解析;(3)y=![]()
【解析】(1)解:(1)由翻折的性质可知,∠BEC=∠FEC,EB=EF
∵AF∥CE
∴∠BEC=∠EAF,∠FEC=∠EFA
∴∠EAF=∠EFA
∴EA=EF
∴EA=EB,即点E为AB的中点
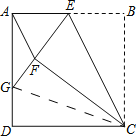
(2)如图所示,连接CG
在正方形ABCD中,∠D=∠B=90°,DC=BC
由翻折的性质可知:∠EFC=∠B=90°,BC=FC
∴∠GFC=∠D,FC=DC
在Rt△GDC和Rt△GEC中,FC=DC,GC=GC
∴Rt△GFC≌Rt△GDC(HL)
∴GF=GD
(3)在Rt△AEG中,AG=10-x,AE=10-y,GE=x+y
由勾股定理可知:AG2+AE2=GE2,即:(10-x)2+(10-y)2=(x+y)2
∴y=![]()


科目:初中数学 来源: 题型:
【题目】(1)一个两位数A,十位数字为a,个位数字为b,交换a和b的位置,得到一个新的两位数B,则A+B一定能被______整除,A-B一定能被______整除;
(2)一个三位数M,百位数字为a,十位数字为b,个位数字为c(a,b,c均为1至9的整数),交换a和c的位置,得到一个新的三位数N.请用含a、b、c的式子分别表示数N与M-N;
(3) 若(2)中a比b大1,M比N大792,求M.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产![]() 两种产品共60件,需购买甲、乙两种材料.生产一件
两种产品共60件,需购买甲、乙两种材料.生产一件![]() 产品需甲种材料4千克;生产一件
产品需甲种材料4千克;生产一件![]() 产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产![]() 产品不少于38件,问符合生产条件的生产方案有哪几种?
产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件![]() 产品需加工费40元,生产一件
产品需加工费40元,生产一件![]() 产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,3),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,3),点B的坐标为(n,1).
(1)求n的值,并结合图象,直接写出不等式![]() <kx+b的解集;
<kx+b的解集;
(2)点E为x轴上一个动点,若S△AEB=6,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB是平角,OD是∠AOC的角平分线,∠COE=∠BOE.

(1)若∠AOC= 50°,则∠DOE= °;
(2)当∠AOC的大小发生改变时,∠DOE的大小是否发生改变?为什么?
(3)图中与∠COD互补角的个数随∠AOC的度数变化而变化,直接写出与∠COD互补的角的个数及对应的∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程(组)与不等式(组)是代数的重要组成部分,也是解决数学问题的重要工具,请利用所学,解决以下 3 个问题:
(1)当 k 为何整数时,关于 x , y 的方程组![]() 的解满足 x y 且 x y 4 ;
的解满足 x y 且 x y 4 ;
(2)已知正整数 a ,使得关于 x , y 的方程组![]() 的解是整数,解关于 x 的不等式
的解是整数,解关于 x 的不等式![]() ;
;
(3)已知 x ,y ,z 为 3 个非负实数,且满足3x 2 y z 5 ,x y z 2 ,记 S 2x y z对于符合题意的任意实数 S ,不等式 2m S 3 始终成立,试确定 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了防止水土流失,某村开展绿化荒山活动,计划经过若干年使本村绿化总面积新增360万平方米.自2014年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.问实际每年绿化面积多少万平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰三角形ABC中,AB=AC=10,BC=12,D为BC边上的任意一点,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E,F,则DE+DF=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
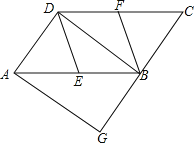
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com