
【题目】方程(组)与不等式(组)是代数的重要组成部分,也是解决数学问题的重要工具,请利用所学,解决以下 3 个问题:
(1)当 k 为何整数时,关于 x , y 的方程组![]() 的解满足 x y 且 x y 4 ;
的解满足 x y 且 x y 4 ;
(2)已知正整数 a ,使得关于 x , y 的方程组![]() 的解是整数,解关于 x 的不等式
的解是整数,解关于 x 的不等式![]() ;
;
(3)已知 x ,y ,z 为 3 个非负实数,且满足3x 2 y z 5 ,x y z 2 ,记 S 2x y z对于符合题意的任意实数 S ,不等式 2m S 3 始终成立,试确定 m 的取值范围.
【答案】(1) -6<k<-4;(2) x≥1;(3) m≤![]() .
.
【解析】
(1)将k看做已知数求出方程组的解表示出x与y,根据题意列出不等式组,求出不等式组的解集即可;
(2)将a看做已知数求出方程组的解表示出x与y,代入不等式,解不等式即可;
(3)解方程组得到x,y,z,再解不等式组,得到S,代入不等式解答即可.
解:(1)解方程组![]() 得
得![]() ,
,
∵x>y且x-y<4,
∴![]() ,
,
解答:-6<k<-4;
(2)解方程组![]() 得,
得, ,
,
∵a为正整数,x、y为整数,
∴a=2,
把a=2代入![]() ≤
≤![]() 得
得![]() ≤
≤![]() ,
,
解得:x≥1;
(3)解方程组
得, ,
,
∵x,y,z为3个非负实数,
∴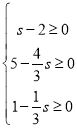 ,解得:2≤S≤3,
,解得:2≤S≤3,
∴S最小=2,S的最大值3,
∵2m-S≤3始终成立,
∴2m-3≤2,
解得:m≤![]() .
.


科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m).
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图8,AB两地之间有一座山,以前从A地到B地需要经过C地.现在政府出资打通了一条山岭隧道,使从A地到B地可沿直线AB直接到达.已知BC=8km,∠A=45°,∠B=53°.
(1)求点C到直线AB的距离;
(2)求现在从A地到B地可比原来少走多少路程?(结果精确到0.1km;参考数据:![]() ≈1.41,sin53°≈0.80,cos53°≈0.60)
≈1.41,sin53°≈0.80,cos53°≈0.60)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若有理数a,b满足等式![]() ,则称a,b是“雉水有理数对”,记作
,则称a,b是“雉水有理数对”,记作![]() 如:数对
如:数对![]() ,
,![]() 都是“雉水有理数对”.
都是“雉水有理数对”.
![]() 数对
数对![]() ______
______![]() 填“是”或“不是”
填“是”或“不是”![]() “雉水有理数对”;
“雉水有理数对”;
![]() 若
若![]() 是“雉水有理数对”,求m的值;
是“雉水有理数对”,求m的值;
![]() 请写出一个符合条件的“锥水有理数对”______
请写出一个符合条件的“锥水有理数对”______![]() 注意:不能与题目中已有的“雉水有理数对”重复
注意:不能与题目中已有的“雉水有理数对”重复![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
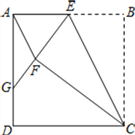
【题目】如图,正方形ABCD中,点E为AB上一动点(不与A、B重合).将△EBC沿CE翻折至△EFC,延长EF交边AD于点G.
(1)连结AF,若 AF∥CE.证明:点E为AB的中点;
(2)证明:GF=GD;
(3)若AD=10,设EB=x,GD=y,求y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)对于任意正实数a、b,
∵(![]() ﹣
﹣![]() )2≥0,
)2≥0,
∴a﹣2![]() +b≥0,
+b≥0,
∴a+b≥2![]() ,(只有当a=b时,a+b等于2
,(只有当a=b时,a+b等于2![]() ).
).
(1)(获得结论)在a+b≥2![]() (a、b均为正实数)中,若ab为定值p,
(a、b均为正实数)中,若ab为定值p,
则a+b≥2![]() ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2![]() .
.
根据上述内容,回答下列问题:若m>0,只有当m= 时,m+![]() 有最小值 .
有最小值 .
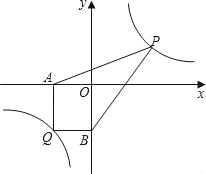
(2)(探索应用)已知点Q(﹣3,﹣4)是双曲线y=![]() 上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=![]() (x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
(x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在数轴上表示的数分别为﹣12和8,两只蚂蚁M、N分别从A、B两点同时匀速出发,同向而行
时间/秒 | 0 | 1 | 5 |
A点位置 | ﹣12 | ﹣9 |
|
B点位置 | 8 |
| 18 |
(1)请填写表格;
(2)若两只蚂蚁在数轴上点P相遇,求点P在数轴上表示的数;
![]()
(3)若运动t秒钟时,两只蚂蚁的距离为10,求出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 两点在数轴上所表示的数分别为
两点在数轴上所表示的数分别为![]() 且满足
且满足![]() .
.
(1)则![]() ,
,![]() ;
;
(2)若点![]() 从
从![]() 点出发,以每秒1个单位长度的速度向右运动,同时点Q从M点出发,以每秒1个单位长度的速度向左运动,经过多长时间后
点出发,以每秒1个单位长度的速度向右运动,同时点Q从M点出发,以每秒1个单位长度的速度向左运动,经过多长时间后![]() 两点相距7个单位长度?
两点相距7个单位长度?
(3)若![]() 为线段
为线段![]() 上的两点,且
上的两点,且![]() ,点
,点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向左运动,点
出发,以每秒2个单位长度的速度向左运动,点![]() 从
从![]() 点出发,以每秒4个单位长度的速度向右运动,点R从B点出发,以每秒3个单位长度的速度向右运动,P,Q,R同时出发,是否存在常数
点出发,以每秒4个单位长度的速度向右运动,点R从B点出发,以每秒3个单位长度的速度向右运动,P,Q,R同时出发,是否存在常数![]() ,使得
,使得![]()
![]() 的值与它们的运动时间无关,为定值。若存在,请求出
的值与它们的运动时间无关,为定值。若存在,请求出![]() 和这个定值;若不存在,请说明理由.
和这个定值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com