
【题目】如图,反比例函数y=![]() 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,3),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,3),点B的坐标为(n,1).
(1)求n的值,并结合图象,直接写出不等式![]() <kx+b的解集;
<kx+b的解集;
(2)点E为x轴上一个动点,若S△AEB=6,求点E的坐标.

【答案】(1)n=6,x<0或2<x<6;(2)E点坐标为(8,0)或(﹣4,0).
【解析】
(1)先把A点坐标代入y=![]() 求出m得到反比例函数解析式为y=
求出m得到反比例函数解析式为y=![]() ,再把B(n,1)代入y=
,再把B(n,1)代入y=![]() 可求出n,然后利用函数图象写出一次函数图象在反比例函数图象上方所对应的自变量的范围即可;
可求出n,然后利用函数图象写出一次函数图象在反比例函数图象上方所对应的自变量的范围即可;
(2)易得直线AB的解析式为y=﹣![]() x+4,再求出直线AB与x轴的交点坐标为(2,0),设E(x,0),利用三角形面积公式得到
x+4,再求出直线AB与x轴的交点坐标为(2,0),设E(x,0),利用三角形面积公式得到![]() ×|x﹣2|×(3﹣1)=6,然后解方程求出x即可得到E点坐标.
×|x﹣2|×(3﹣1)=6,然后解方程求出x即可得到E点坐标.
(1)把A(2,3)代入y=![]() 得m=2×3=6,
得m=2×3=6,
∴反比例函数解析式为y=![]() ,
,
把B(n,1)代入y=![]() 得n=6,
得n=6,
当2<x<6或x<0时,![]() <kx+b,
<kx+b,
即不等式![]() <kx+b的解集为x<0或2<x<6;
<kx+b的解集为x<0或2<x<6;
(2)易得直线AB的解析式为y=﹣![]() x+4,
x+4,
当x=0时,﹣![]() x+4=0,解得x=8,则直线AB与x轴的交点坐标为(8,0)
x+4=0,解得x=8,则直线AB与x轴的交点坐标为(8,0)
设E(x,0),
∴![]() ×|x﹣8|×(3﹣1)=6,解得x=14或x=2
×|x﹣8|×(3﹣1)=6,解得x=14或x=2
∴E点坐标为(14,0)或(2,0).


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:初中数学 来源: 题型:
【题目】将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,…则第n个图形有__个小圆.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个已知图形G1、G2,在G1上任取一点P,在G2上任取一点Q,当线段PQ的长度最小时,我们称这个最小长度为G1、G2的“密距”.例如,如图,A(﹣2,3),B(1,3),C(1,0),则点A与射线OC之间的“密距”为![]() ,点B与射线OC之间的“密距”为3.如果直线y=x﹣1和双曲线y=
,点B与射线OC之间的“密距”为3.如果直线y=x﹣1和双曲线y=![]() 之间的“密距”为
之间的“密距”为![]() ,则k值为_____.
,则k值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图8,AB两地之间有一座山,以前从A地到B地需要经过C地.现在政府出资打通了一条山岭隧道,使从A地到B地可沿直线AB直接到达.已知BC=8km,∠A=45°,∠B=53°.
(1)求点C到直线AB的距离;
(2)求现在从A地到B地可比原来少走多少路程?(结果精确到0.1km;参考数据:![]() ≈1.41,sin53°≈0.80,cos53°≈0.60)
≈1.41,sin53°≈0.80,cos53°≈0.60)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若有理数a,b满足等式![]() ,则称a,b是“雉水有理数对”,记作
,则称a,b是“雉水有理数对”,记作![]() 如:数对
如:数对![]() ,
,![]() 都是“雉水有理数对”.
都是“雉水有理数对”.
![]() 数对
数对![]() ______
______![]() 填“是”或“不是”
填“是”或“不是”![]() “雉水有理数对”;
“雉水有理数对”;
![]() 若
若![]() 是“雉水有理数对”,求m的值;
是“雉水有理数对”,求m的值;
![]() 请写出一个符合条件的“锥水有理数对”______
请写出一个符合条件的“锥水有理数对”______![]() 注意:不能与题目中已有的“雉水有理数对”重复
注意:不能与题目中已有的“雉水有理数对”重复![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
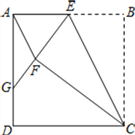
【题目】如图,正方形ABCD中,点E为AB上一动点(不与A、B重合).将△EBC沿CE翻折至△EFC,延长EF交边AD于点G.
(1)连结AF,若 AF∥CE.证明:点E为AB的中点;
(2)证明:GF=GD;
(3)若AD=10,设EB=x,GD=y,求y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com