
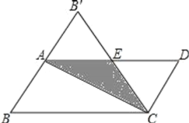
【题目】如图,在平行四边形纸片ABCD中,AB=3,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则图中重叠部分的面积为_____.
【答案】![]() .
.
【解析】
根据翻折的性质,及已知的角度,可得△AEB’为等边三角形,再由四边形ABCD为平行四边形,且∠B=60°,从而知道B’,A,B三点在同一条直线上,再由AC是对称轴,所以AC垂直且平分BB’,AB=AB’=AE=3,求AE边上的高,从而得到面积.
解:∵△CDE恰为等边三角形,
∴∠AEB’=∠DEC=60°,∠D=∠B=∠B’=60°,
∴△AEB’为等边三角形,
由四边形ABCD为平行四边形,且∠B=60°,
∴∠BAD=120°,所以所以∠B’AE+∠DAB=180°,
∴B’,A,B三点在同一条直线上,
∴AC是对折线,
∴AC垂直且平分BB’,
∴AB=AB’=AE=3,AE边上的高,h=CD×sin60°=![]() ,
,
∴面积为![]() .
.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】小明在一次打篮球时,篮球传出后的运动路线为如图所示的抛物线,以小明所站立的位置为原点O建立平面直角坐标系,篮球出手时在O点正上方1m处的点P.已知篮球运动时的高度y(m)与水平距离x(m)之间满足函数表达式y=-![]() x2+x+c.
x2+x+c.
(1)求y与x之间的函数表达式;
(2)球在运动的过程中离地面的最大高度;
(3)小亮手举过头顶,跳起后的最大高度为BC=2.5m,若小亮要在篮球下落过程中接到球,求小亮离小明的最短距离OB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E,某同学分析图形后得出以下结论,上述结论一定正确的是______(填代号).
①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形;
(2)连接CF,若∠ABC=60°,AB= 4,AF =2DF,求CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:直线AB、CD相交于点O;
(1)若∠AOC=30°,则∠BOC= °,∠BOD= °;
(2)将直线CD绕点O旋转,请根据下表所给数据将表格补充完整;
∠AOC | 60° | 90° | x° |
∠BOD |
|
|
|
(3)如图3,过点O分别作∠AOC与∠AOD的角分线OE、OF,若∠BOD的度数为α,请用含α的代数式表示∠COF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
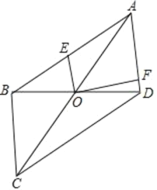
【题目】如图,在平行四边形ABCD中,对角线AC与BD相交于点O,AB=5,AD=3,E是AB上的一点,F是AD上的一点,连接BO和FO.
(1)当点E为AB中点时,求EO的长度;
(2)求线段AO的取值范围;
(3)当EO⊥FO时,连接EF.求证:BE+DF>EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形纸片ABCD中,AB=3,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则图中重叠部分的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.
(1)求证:AB=AF;
(2)若BC=2AB,∠BCD=110°,求∠ABE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com