
【题目】如图:直线AB、CD相交于点O;
(1)若∠AOC=30°,则∠BOC= °,∠BOD= °;
(2)将直线CD绕点O旋转,请根据下表所给数据将表格补充完整;
∠AOC | 60° | 90° | x° |
∠BOD |
|
|
|
(3)如图3,过点O分别作∠AOC与∠AOD的角分线OE、OF,若∠BOD的度数为α,请用含α的代数式表示∠COF的度数.

【答案】(1)150°,30°.(2)60°,90°,x°.(3)∠COF=90°+![]() α.
α.
【解析】
(1)根据平角等于180°,利用角的和差即可得出答案;
(2)同(1)的计算方法即可得出答案;
(3)首先证明∠EOF=90°,利用(2)中结论求出∠EOC即可解决问题.
解:(1)如图1中,∵∠AOC=30°,
∴∠BOC=∠AOB-∠AOC
=180°-30°
=150°,
∠BOD=∠COD-∠BOC=180°﹣150°=30°,
故答案为150°,30°.
(2)由(1)可知∠AOC+∠BOC=180°,∠BOD+∠BOC=180°,
∴∠BOD=∠AOC(同角的补角相等),
∴当∠AOC=60°时,∠BOD=60°,
当∠AOC=90°时,∠BOD=90°,
当∠AOC=x°时,∠BOD=x°,
故答案为60°,90°,x°.
(3)∵∠AOC=∠BOD,∠BOD=α,
∴∠AOC=α,
∵OE平分∠AOC,
∴∠EOC=![]() α,
α,
∵OF平分∠AOD,
∴∠AOF=![]() ∠AOD,∠AOE=
∠AOD,∠AOE=![]() ∠AOC,
∠AOC,
∴∠EOF=∠AOE+∠AOF=![]() ∠COD=90°,
∠COD=90°,
∴∠COF=90°+![]() α.
α.


科目:初中数学 来源: 题型:
【题目】已知正方体的展开图如图所示,如果正方体的六个面分别用字母A,B,C,D,E,F表示,当各面上的数分别与它对面的数互为相反数,且满足B=1,C=﹣a2﹣2a+1,D=﹣1,E=3a+4,F=2﹣a时,求A面表示的数值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+2的图象与反比例函数y=﹣![]() 的图象交于A、B两点,与x轴交于D点,且C、D两点关于y轴对称.
的图象交于A、B两点,与x轴交于D点,且C、D两点关于y轴对称.
(1)求A、B两点的坐标;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图所示的图形,回答下列问题:
(1)按甲方式将桌子拼在一起.
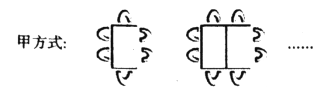
4张桌子拼在一起共有 个座位,n张桌子拼在一起共有 个座位;
(2)按乙方式将桌子拼在一起.
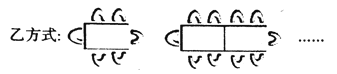
6张桌子拼在一起共有 个座位,m张桌子拼在一起共有 个座位;
(3)某食堂有A,B两个餐厅,现有102张这样的长方形桌子,计划把这些桌子全放在两个餐厅,每个餐厅都要放有桌子.将a张桌子放在A餐厅,按甲方式每6张拼成1张大桌子;将其余桌子都放在B餐厅,按乙方式每4张桌子拼成1张大桌子,若两个餐厅一共有404个座位,问A,B两个餐厅各有多少个座位?
查看答案和解析>>
科目:初中数学 来源: 题型:
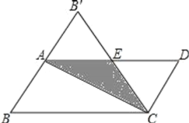
【题目】如图,在平行四边形纸片ABCD中,AB=3,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则图中重叠部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一根起点为1的数轴,现有同学将它弯折,弯折后虚线上由左至右第1个数是1,第2个数是13,第3个数是41,…,依此规律,第5个数是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为原点,A、B为数轴上两点,点A表示的数a,点B表示的数是b,且![]() .
.
![]()
(1)a= ,b= ;
(2)在数轴上是否存在一点P,使![]() ,若有,请求出点P表示的数,若没有,请说明理由?
,若有,请求出点P表示的数,若没有,请说明理由?
(3)点M从点A出发,沿![]() 的路径运动,在路径
的路径运动,在路径![]() 的速度是每秒2个单位,在路径
的速度是每秒2个单位,在路径![]() 上的速度是每秒4个单位,同时点N从点B出发以每秒3个单位长向终点A运动,当点M第一次回到点A时整个运动停止.几秒后MN=1?
上的速度是每秒4个单位,同时点N从点B出发以每秒3个单位长向终点A运动,当点M第一次回到点A时整个运动停止.几秒后MN=1?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)﹣12+3×(﹣2)3﹣(﹣6)÷(﹣![]() )2;
)2;
(2)﹣2﹣12×(![]() );
);
(3)3x2+(2x2﹣3x)﹣(﹣x+5x2);
(4)5(3a2b﹣ab2)﹣4(﹣ab2+3a2b).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1所示的三棱柱,高为8cm,底面是一个边长为5cm的等边三角形.
(1)这个三棱柱有 条棱,有 个面;
(2)图2框中的图形是该三棱柱的一种表面展开图的一部分,请将它补全(一种即可);
(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,至少需剪开 条棱,需剪开棱的棱长的和的最大值为 cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com