
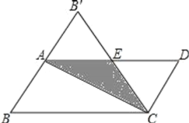
【题目】如图,在平行四边形纸片ABCD中,AB=3,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则图中重叠部分的面积为_____.

【答案】![]() .
.
【解析】
根据翻折的性质,及已知的角度,可得△AEB’为等边三角形,再由四边形ABCD为平行四边形,且∠B=60°,从而知道B’,A,B三点在同一条直线上,再由AC是对称轴,所以AC垂直且平分BB’,AB=AB’=AE=3,求AE边上的高,从而得到面积.
解:∵△CDE恰为等边三角形,
∴∠AEB’=∠DEC=60°,∠D=∠B=∠B’=60°,
∴△AEB’为等边三角形,
由四边形ABCD为平行四边形,且∠B=60°,
∴∠BAD=120°,所以所以∠B’AE+∠DAB=180°,
∴B’,A,B三点在同一条直线上,
∴AC是对折线,
∴AC垂直且平分BB’,
∴AB=AB’=AE=3,AE边上的高,h=CD×sin60°=![]() ,
,
∴面积为![]() .
.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
【题目】为了解学生课余活动情况,某班对参加A组:绘画;B组:书法;C组:舞蹈;D组:乐器;这四个课外兴趣小组的人员分布情况进行抽样调查,并根据收集的数据绘制了如图两幅不完整的统计图,请根据图中提供信息,解答下面的问题:
(1)此次共调查了多少名同学?
(2)将条形统计图补充完整,
(3)计算扇形统计图中书法部分的圆心角的度数;
(4)已知在此次调查中,参加D组的5名学生中有3名女生和2名男生,要从这5名学生中随机抽取2名学生参加市举办的音乐赛,用列表法或画树状图的方法求出抽取的2名学生恰好是1男1女的概率。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形纸片ABCD中,AB=3,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则图中重叠部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为原点,A、B为数轴上两点,点A表示的数a,点B表示的数是b,且![]() .
.
![]()
(1)a= ,b= ;
(2)在数轴上是否存在一点P,使![]() ,若有,请求出点P表示的数,若没有,请说明理由?
,若有,请求出点P表示的数,若没有,请说明理由?
(3)点M从点A出发,沿![]() 的路径运动,在路径
的路径运动,在路径![]() 的速度是每秒2个单位,在路径
的速度是每秒2个单位,在路径![]() 上的速度是每秒4个单位,同时点N从点B出发以每秒3个单位长向终点A运动,当点M第一次回到点A时整个运动停止.几秒后MN=1?
上的速度是每秒4个单位,同时点N从点B出发以每秒3个单位长向终点A运动,当点M第一次回到点A时整个运动停止.几秒后MN=1?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校要购入两种记录本,其中A种记录本每本3元,B种记录本每本2元,且购买A种记录本的数量比B种记录本的2倍还多20本,总花费为460元.
(1)求购买B种记录本的数量;
(2)某商店搞促销活动,A种记录本按8折销售,B种记录本按9折销售,则学校此次可以节省多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)﹣12+3×(﹣2)3﹣(﹣6)÷(﹣![]() )2;
)2;
(2)﹣2﹣12×(![]() );
);
(3)3x2+(2x2﹣3x)﹣(﹣x+5x2);
(4)5(3a2b﹣ab2)﹣4(﹣ab2+3a2b).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.

(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,BC∥OA,BC=3,OA=6,AB=3![]()
(1)直接写出点B的坐标
(2)已知D.E分别为线段OC.OB上的点,OD=5,OE=2BE,直线DE交x轴于点F,求直线DE的解析式
(3)在(2)的条件下,点M是直线DE上的一点,在x轴上方是否存在另一个点N,使以O.D.M.N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com