Question

【题目】△ABC是一块锐角三角形余料，边BC=180mm，高AD=120mm，要把它加工成矩形零件，使一边在BC上，其余两个顶点分别在边AB、AC上．

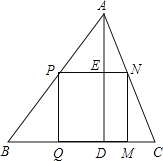
（1）若这个矩形是正方形，那么边长是多少？

（2）若这个矩形的长是宽的2倍，则边长是多少？

Answer 1

【答案】（1）72mm．（2）矩形的长为90mm，宽是45mm或者长为mm，宽为mm．

【解析】

试题分析：（1）设出边长为xmm，由正方形的性质得出PN∥BC，PQ∥AD，根据平行线的性质，可以得出比例关系式，=、=，代入数据求解即可．

（2）设宽为xmm，则长为2xmm，同（1）列出比例关系求解，但是要注意有两种情况，PQ可以为长也可以为宽，分两种情况分别求解即可．

解：（1）设边长为xmm，

∵矩形为正方形，

∴PN∥BC，PQ∥AD，

根据平行线的性质可以得出：=、=，

由题意知PQ=x，BC=180mm，AD=120mm，PN=x，

即=，=，

∵AP+BP=AB，

∴+=+=1，

解得x=72．

答：若这个矩形是正方形，那么边长是72mm．

（2）设边宽为xmm，则长为2xmm，

∵四边形PNMQ为矩形，

∴PN∥BC，PQ∥AD，

根据平行线的性质可以得出：=、=，

①PQ为长，PN为宽：

由题意知PQ=2xmm，AD=120mm，BC=180mm，AN=xmm，

即=，=，

∵AP+BP=AB，

∴+=+=1，

解得x=45，2x=90．

即长为90mm，宽为45mm．

②PQ为宽，PN为长：

由题意知PQ=xmm，AD=120mm，BC=180mm，PN=2xmm，

即=，=，

∵AP+BP=AB，

∴+=+=1，

解得x=，2x=．

即长为mm，宽为mm．

答：矩形的长为90mm，宽是45mm或者长为mm，宽为mm．