
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.

(1)当∠BDA=115°时,∠EDC=____ __,∠DEC=__ ___;点D从B向C运动时,∠BAD逐渐变_______(填“大”或“小”),∠BAD_______∠CDE(填“=”或“>”或“<”).
(2)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
【答案】(1)25°,115°,大;=;(2)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形.
【解析】
(1)根据∠BDA=115°以及∠ADE=40°,即可得出∠EDC=180°∠BDA∠ADE,进而求出∠DEC的度数;然后观察图形,根据三角形内角和定理及平角的概念可得∠BAD逐渐变大,∠BAD=∠CDE;
(2)分情况讨论:①当AD=AE时,②当DA=DE时,③当EA=ED时,分别利用三角形外角的性质和三角形内角和定理进行求解即可.
解:(1)∠EDC=180°∠BDA∠ADE=180°115°40°=25°,
∠DEC=180°∠EDC∠C=180°25°40°=115°;
观察图形可得:点D从B向C运动时,∠BAD逐渐变大,
在△ABD中,∠BAD=180°-∠ABD-∠BDA=180°-40°-∠BDA,
∵∠CDE=180°-∠BDA-∠ADE=180°-40°-∠BDA,
∴∠BAD=∠CDE;
故答案为:25°,115°,大;=;
(2)分情况讨论:
①当AD=AE时,则∠ADE=∠AED=40°,
∵∠AED>∠C=40°,
∴此情况不成立;
②当DA=DE时,即∠DAE=∠DEA=![]() (180°40°)=70°,
(180°40°)=70°,
∠BDA=∠DAE+∠C=70°+40°=110°;
③当EA=ED时,∠ADE=∠DAE=40°,
∠BDA=∠DAE+∠C=40°+40°=80°,
综上所述:当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形.


科目:初中数学 来源: 题型:
【题目】某教育科技公司销售A,B两种多媒体,这两种多媒体的进价与售价如表所示:

该教育科技公司计划购进两种多媒体共50套,共需资金132万元 .
(1)该教育科技公司计划购进A,B两种多媒体各多少套?
(2)经过市场调查后,该商店决定在原计划50套多媒体的基础上,减少A的购进数量,增加B 的购进数量,已知B种多媒体增加的数量是A种多媒体减少数量的1.5倍,全部销售后可以获取毛利润21万元,问实际购进A种多媒体多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家公司共有150名工人,甲公司每名工人月工资为1200元,乙公司每名工人月工资为1500元,两家公司每月需付给工人工资共计19.5万元.
(1)求甲、乙公司分别有多少名工人;
(2)经营一段时间后发现,乙公司工人人均月产值是甲公司工人的3.2倍,于是甲公司决定内部调整,选拔了本公司部分工人到新岗位工作.调整后,原岗位工人和新岗位工人的人均月产值分别为调整前的1.2倍和4倍,且甲公司新岗位工人的月生产总值不超过乙公司月生产总值的40%,甲公司的月生产总值不少于乙公司的月生产总值,求甲公司选拔到新岗位有多少人?(甲公司调整前人均月产值设定为p元)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师将1个黑球和若干个白球入放一个不透明的口袋并搅匀,让若干学生进行摸球试验,每次摸出一个球(有放回),统计数据如下表:
摸球的次数(n) | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数(m) | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率(m/n) | 0.230 | 0.207 | 0.300 | 0.260 | 0.254 |
(1)补全上表中的有关数据,并根据上表数据估计从袋中摸出一个球是黑球的概率是 ;
(2)估计口袋中白球的个数;
(3)在(2)的条件下,若小强同学有放回地连续两次摸球,用画树状图法或列表法计算他两次都摸出白球的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
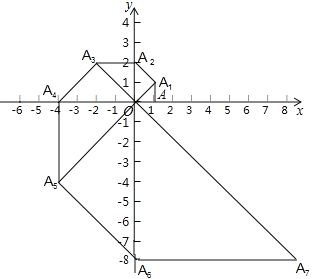
【题目】如图,在平面直角坐标系中,等腰直角三角形OAA1的直角边OA在x轴上,点A1在第一象限,且OA=1,以点A1为直角顶点,0A1为一直角边作等腰直角三角形OA1A2,再以点A2为直角顶点,OA2为直角边作等腰直角三角形OA2A3…依此规律,则点A2019的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图线段AB的端点在边长为1的正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.

(1)请你用尺规在所给的网格中画出线段AC及点B经过的路径;
(2)若将此网格放在一平面直角坐标系中,已知点A的坐标为(1,3),点B的坐标为(-2,-1),则点C的坐标为 ;
(3)线段AB在旋转到线段AC的过程中,线段AB扫过的区域的面积为 ;
(4)若有一张与(3)中所说的区域形状相同的纸片,将它围成一个几何体的侧面,则该几何体底面圆的半径长为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC是等腰三角形,AB=AC,点D,E,F分别在AB,BC,AC边上,且BD=CE,BE=CF.
(1)求证:△DEF是等腰三角形;
(2)猜想:当∠A满足什么条件时,△DEF是等边三角形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的![]() ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com