
【题目】甲、乙两家公司共有150名工人,甲公司每名工人月工资为1200元,乙公司每名工人月工资为1500元,两家公司每月需付给工人工资共计19.5万元.
(1)求甲、乙公司分别有多少名工人;
(2)经营一段时间后发现,乙公司工人人均月产值是甲公司工人的3.2倍,于是甲公司决定内部调整,选拔了本公司部分工人到新岗位工作.调整后,原岗位工人和新岗位工人的人均月产值分别为调整前的1.2倍和4倍,且甲公司新岗位工人的月生产总值不超过乙公司月生产总值的40%,甲公司的月生产总值不少于乙公司的月生产总值,求甲公司选拔到新岗位有多少人?(甲公司调整前人均月产值设定为p元)
【答案】(1)甲公司有100名工人,乙公司有50名工人;(2)甲公司选拔15人或16人到新岗位工作.
【解析】
试题
(1)设甲公司有x名工人,乙公司有y名工人,由题意可列二元一次方程组,解方程组即可得到两公司各有多少工人;
(2)设甲公司选拔了a人到新岗位工作,甲公司调整前人均月产值为p元,则甲公司在原岗位工作的有(100-a)人,调整后,新岗位每人产值为4p元,原岗位每人产值为1.2p元,乙公司月生产总值为3.2p×50元,根据题意列出不等式组,解不等式组并求得其整数解即可得到所求答案.
试题解析:
解:(1)设甲公司有x名工人,乙公司有y名工人,
由题意得:![]() ,解得:
,解得:![]() .
.
即甲公司有100名工人,乙公司有50名工人.
(2)设甲公司选拔a人到新岗位工作,甲公司调整前人均月产值为p元,
由题意得:![]() ,解得:
,解得:![]() ,
,
又∵![]() 为整数,
为整数,
∴![]() =15或16,
=15或16,
答:甲公司选拔15人或16人到新岗位工作.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知,如图矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF.
(1)求证:BE=BF;
(2)求△ABE的面积;
(3)求折痕EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON及其边上一点A,以点A为圆心,AO长为半径画弧,分别交OM,ON于点B和C,再以点C为圆心,AC长为半径画弧,恰好经过点B,错误的结论是( ).
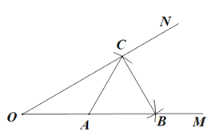
A.![]() B.∠OCB=90°C.∠MON=30°D.OC=2BC
B.∠OCB=90°C.∠MON=30°D.OC=2BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多创新与发展都曾居世界前列,其中“杨辉三角”(如图)就是一例,它的发现比欧洲早五百年左右.

杨辉三角两腰上的数都是1,其余每个数为它的上方(左右)两数之和.事实上,这个三角形给出了![]() (n=1,2,3,4,5,6)的展开式(按a的次数由大到小的顺序排列)的系数规律. 例如,在三角形中第三行的三个数1,2,1,恰好对应着
(n=1,2,3,4,5,6)的展开式(按a的次数由大到小的顺序排列)的系数规律. 例如,在三角形中第三行的三个数1,2,1,恰好对应着![]() 展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着![]() 展开式中各项的系数,等等.
展开式中各项的系数,等等.
(1)当n=4时,![]() 的展开式中第3项的系数是_________;
的展开式中第3项的系数是_________;
(2)人们发现,当n是大于6的自然数时,这个规律依然成立,那么![]() 的展开式中各项的系数的和为_________.
的展开式中各项的系数的和为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=![]() ,AC=2,将线段AC绕点A按逆时针方向旋转60°至AD,D恰在BC的延长线上,则下列关于此图形的一些说法中正确的有( )
,AC=2,将线段AC绕点A按逆时针方向旋转60°至AD,D恰在BC的延长线上,则下列关于此图形的一些说法中正确的有( )
(1)△ACD是等边三角形;(2)∠B=30°;
(3)△ABD是直角三角形;(4)点C是BD的中点.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点坐标是(2,﹣1),且经过点A(5,8)
(1)求该抛物线的解析式;
(2)设该抛物线与y轴相交于点B,与x轴相交于C、D两点(点C在点D的左边),试求点B、C、D的坐标;
(3)设点P是x轴任一点,连接AP、BP.试求当AP+BP取得最小值时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点都在方格线的交点(格点)上.
(1)将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′,请在图中画出△A′B′C′.
(2)将△ABC向上平移1个单位,再向右平移5个单位得到△A″B″C″,请在图中画出△A″B″C″.
(3)若将△ABC绕原点O旋转180°,A的对应点A1的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.

(1)当∠BDA=115°时,∠EDC=____ __,∠DEC=__ ___;点D从B向C运动时,∠BAD逐渐变_______(填“大”或“小”),∠BAD_______∠CDE(填“=”或“>”或“<”).
(2)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑期,某学校将组织部分优秀学生分别到A、B、C、D四个地方进行夏令营活动,学校按定额购买了前往四地的车票.如图1是未制作完成的车票种类和数量的条形统计图,请根据统计图回答下列问题:
(1)若去C地的车票占全部车票的30%,则去C地的车票数量是 张,补全统计图;
(2)若学校采用随机抽取的方式分发车票,每人一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么李明同学抽到去B地的概率是多少?
(3)若有一张去A地的车票,红红和天天都想要,决定采取旋转转盘的方式来确定.其中甲转盘被分成四等份且标有数字1、2、3、4,乙转盘分成三等份且标有数字7、8、9,如图2所示.具体规定是:同时转动两个转盘,当指针指向的两个数字之和是偶数时,票给红红,否则票给天天(指针指在线上重转).试用“列表法”或“树状图”的方法分析这个规定对双方是否公平.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com