练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，A、F、B、C是半圆O上的四个点，四边形OABC是平行四边形，∠FAB＝15°，连接OF交AB于点E，过点C作CD∥OF交AB的延长线于点D，延长AF交直线CD于点H.

    （1）求证：CD是半圆O的切线；

    （2）若DH＝，求EF的长和半径OA的长.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016年初中毕业升学考试（吉林长春卷）数学（解析版） 题型：解答题

    如图．在□ABCD中，点E在边BC上，点F在边AD的延长线上，且DF=BE．EF与CD交于点G．

    （1）求证：BD∥EF ．

    （2）若，BE=4，求EC的长．

    查看答案和解析>>

    科目：初中数学 来源：2016年初中毕业升学考试（湖南张家界卷）数学（解析版） 题型：选择题

    下列运算正确的是（ ）

    A．（x﹣y）2=x2﹣y2 B．x2•x4=x6 C． D．（2x2）3=6x6

    查看答案和解析>>

    科目：初中数学 来源：2016年初中毕业升学考试（湖北宜昌卷）数学（解析版） 题型：选择题

    如图，田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能正确解释这一现象的数学知识是（ ）

    A．垂线段最短

    B．经过一点有无数条直线

    C．经过两点，有且仅有一条直线

    D．两点之间，线段最短

    查看答案和解析>>

    科目：初中数学 来源：2016年初中毕业升学考试（湖北宜昌卷）数学（解析版） 题型：选择题

    如图，若要添加一条线段，使之既是轴对称图形又是中心对称图形，正确的添加位置是（ ）

    查看答案和解析>>

    科目：初中数学 来源：2016年初中毕业升学考试（湖北荆州卷）数学（解析版） 题型：填空题

    若函数y=（a﹣1）x2﹣4x+2a的图象与x轴有且只有一个交点，则a的值为 ．

    查看答案和解析>>

    科目：初中数学 来源：2016年初中毕业升学考试（湖北荆州卷）数学（解析版） 题型：填空题

    将二次三项式x2+4x+5化成（x+p）2+q的形式应为 ．

    查看答案和解析>>

    科目：初中数学 来源：2016年初中毕业升学考试（陕西卷）数学（解析版） 题型：解答题

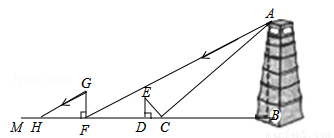
    某市为了打造森林城市，树立城市新地标，实现绿色、共享发展理念，在城南建起了“望月阁”及环阁公园．小亮、小芳等同学想用一些测量工具和所学的几何知识测量“望月阁”的高度，来检验自己掌握知识和运用知识的能力．他们经过观察发现，观测点与“望月阁”底部间的距离不易测得，因此经过研究需要两次测量，于是他们首先用平面镜进行测量．方法如下：如图，小芳在小亮和“望月阁”之间的直线BM上平放一平面镜，在镜面上做了一个标记，这个标记在直线BM上的对应位置为点C，镜子不动，小亮看着镜面上的标记，他来回走动，走到点D时，看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合，这时，测得小亮眼睛与地面的高度ED=1.5米，CD=2米，然后，在阳光下，他们用测影长的方法进行了第二次测量，方法如下：如图，小亮从D点沿DM方向走了16米，到达“望月阁”影子的末端F点处，此时，测得小亮身高FG的影长FH=2.5米，FG=1.65米．

    如图，已知AB⊥BM，ED⊥BM，GF⊥BM，其中，测量时所使用的平面镜的厚度忽略不计，请你根据题中提供的相关信息，求出“望月阁”的高AB的长度．

    查看答案和解析>>

    科目：初中数学 来源：2016年初中毕业升学考试（山东东营卷）数学（解析版） 题型：单选题

    如图，直线m∥n，∠1＝70°，∠2＝30°，则∠A等于（ ）

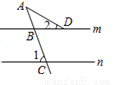
    A. 30° B. 35° C. 40° D. 50°

    查看答案和解析>>

    同步练习册答案