
【题目】在Rt△ABC中,∠C=90°,AC=16cm,BC=12cm.现有动点P从点A出发,沿线段AC向点C方向运动,动点Q从点C出发,沿线段CB向点B方向运动.如果点P的速度是4cm/s,点Q的速度是3cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为ts.
求:(1)用含t的代数式表示Rt△CPQ的面积S;
(2)当t=2s时,P、Q两点之间的距离是多少?
(3)当t为多少秒时,以C、P、Q为顶点的三角形与△ABC相似?
【答案】(1)Rt△CPQ的面积为S=﹣6t2+24t(0<t<4);(2)PQ=10cm;(3)t=2秒或t=![]() 秒时,以点C、P、Q为顶点的三角形与△ABC相似.
秒时,以点C、P、Q为顶点的三角形与△ABC相似.
【解析】
(1)由点P,点Q的运动速度和运动时间,又知AC,BC的长,可将CP.CQ用含t的表达式求出,代入直角三角形面积公式S△CPQ=![]() CP
CP![]() CQ求解
CQ求解
(2)在Rt△CPQ中,当t=2秒,可知CP、CQ的长,运用勾股定理可将PQ的长求出
(3)应分两种情况:当R△CPQ∽R△CAB时根据![]() ,可将时间t求出;当Rt△ CPQ∽Rt△CBA时,根据
,可将时间t求出;当Rt△ CPQ∽Rt△CBA时,根据![]() ,可求出时间t.
,可求出时间t.
(1)由题意得AP=4t,CQ=3t,则CP=16﹣4t,
因此Rt△CPQ的面积为S=![]() CP×CQ=
CP×CQ=![]() (16﹣4t)×3t=﹣6t2+24t(0<t<4);
(16﹣4t)×3t=﹣6t2+24t(0<t<4);
(2)由题意得AP=4t,CQ=3t,则CP=16﹣4t,
当t=2秒时,CP=16﹣4t=8cm,CQ=3t=6cm,
在Rt△CPQ中,由勾股定理得PQ=![]() ;
;
(3)由题意得AP=4t,CQ=3t,则CP=16﹣4t,
∵AC=16cm,BC=12cm.
∴①当Rt△CPQ∽Rt△CAB时,![]() ,即
,即![]() ,解得t=2秒;
,解得t=2秒;
②当Rt△CPQ∽Rt△CBA时,![]()
![]() ,即
,即![]() ,解得t=
,解得t=![]() 秒.
秒.
因此t=2秒或t=![]() 秒时,以点C、P、Q为顶点的三角形与△ABC相似.
秒时,以点C、P、Q为顶点的三角形与△ABC相似.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
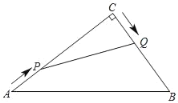
【题目】(1)如图,已知线段![]() 和
和![]() ,请在给出的图形上用尺规作出
,请在给出的图形上用尺规作出![]() ,使得:点
,使得:点![]() 在射线
在射线![]() 上,点
上,点![]() 在射线
在射线![]() 上,且
上,且![]() ,
,![]() ;(保留作图痕迹,不写作法)
;(保留作图痕迹,不写作法)
(2)求证:直角三角形斜边上的中线等于斜边的一半.(要求:利用(1)中的Rt![]() ,画出斜边
,画出斜边![]() 上的中线
上的中线![]() ,写出已知、求证和证明过程)
,写出已知、求证和证明过程)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
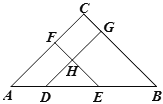
【题目】如图,在△ABC中 ,∠A=∠B,D、E是边AB上的点,DG∥AC,EF∥BC,DG、EF相 交于点H.
(1)∠HDE与∠HED是否相等?并说明理由.
解:∠HDE=∠HED.理由如下:
∵DG∥AC(已知)
∴ = ( )
∵ EF∥BC (已知)
∴ = ( )
又∵∠A=∠B (已知)
∴ = ( ).
(2)如果∠C=90°,DG、 EF有何位置关系?并仿照 (1)中的解答方法说明理由.
解: .理由如下:
查看答案和解析>>
科目:初中数学 来源: 题型:
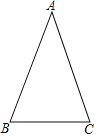
【题目】在△ABC中,AB=AC,∠ABC=70°
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法)
(2)在(1)的条件下,∠BDC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小王在校园上的A处正面观测一座教学楼墙上的大型标牌,测得标牌下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该标牌上端C处的仰角为45°.若该楼高为16.65m,小王的眼睛离地面1.65m,大型标牌的上端与楼房的顶端平齐.求此标牌上端与下端之间的距离(![]() ≈1.732,结果精确到0.1m).
≈1.732,结果精确到0.1m).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车专卖店销售某种型号的汽车.已知该型号汽车的进价为10万元/辆,销售一段时间后发现:当该型号汽车售价定为15万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出2辆.
(1)若要平均每周售出汽车不低于15辆,该汽车的售价最多定为多少万元?
(2)该店计划下调售价,尽可能增加销量,减少库存,但要确保平均每周的销售利润为40万元,每辆汽车的售价定为多少合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以点AB为直径的⊙O分别与AC,BC交于点E,D,且BD=CD.
(1)求证:∠B=∠C .
(2)过点D作DF⊥OD,过点F作FH⊥AB.若AB=5,CD=![]() ,求AH的值.
,求AH的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com